Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

đặt MA= x (cm)
tam giác ABC cân nên : 12-x
diện tích hình bình hành MNCP là : MP.MA = (12-x)x
diện tích bằng 32cm vuông , nê ta có phương trình:
x^2 -12x +32 = 0
giải pt ta được x1= 4 , x2 =8
vậy M cách A là 4cm hoặc 8cm.

4. Dễ thấy \(\Delta AML\approx\Delta LKC\left(g-g\right)\)
\(\Rightarrow\frac{AL}{LC}=\sqrt{\frac{S_{\Delta AML}}{S_{\Delta LKC}}}=\sqrt{\frac{42.7283}{51.4231}}\approx0.9115461896\)
\(\Rightarrow\frac{AL}{AC}=\frac{0.9115461896}{0.9115461896+1}=0.476863282\)
Lại có \(\Delta AML\approx\Delta ABC\left(g-g\right)\)
\(\Rightarrow\frac{S_{AML}}{S_{ABC}}=\left(\frac{AL}{AC}\right)^2=0.476863282^2=0.2273985897\)
\(\Rightarrow S_{\Delta ABC}=\frac{S_{\Delta AML}}{0.2273985897}=\frac{42.7283}{0.2273985897}\approx187.9\left(cm^2\right)\)
1. Ta có \(\frac{BH}{CH}=\frac{\sqrt{7}}{\sqrt{5}}\Rightarrow BH=\frac{\sqrt{7}}{\sqrt{5}}CH\)
Mặt khác \(BC=\sqrt{11}\Rightarrow BH+CH=11\)
\(\Rightarrow\frac{\sqrt{7}}{\sqrt{5}}CH+CH=11\)
\(\Leftrightarrow CH=\frac{-55+11\sqrt{35}}{2}\) và \(BH=\frac{77-11\sqrt{35}}{2}\)
Có BH, CH và BC tính đc AB, AC \(\left(AB=\sqrt{BH.BC};AC=\sqrt{CH.BC}\right)\)
Từ đó tính đc chu vi tam giác ABC.
2. Để cj gửi hình qua gmail cho
3. Chỉ còn cách làm từng bước thôi e
\(B=31+\frac{27}{\frac{30127}{2008}}=31+\frac{54216}{30127}=32+\frac{24089}{30127}\)
Để viết liên phân số, ta bấm phím tìm thương và số dư:
(Mỗi số b1, b2, b3, ..., bn-1 chính là thương; số chia của phép chia trước là số bị chia của phép chia sau, còn số dư của phép chia trước là số chia của phép chia sau, nhớ nhá)
- B1: Tìm thương và số dư của 30127 cho 24089, thương là 1, dư 6038, viết \(B=32+\frac{1}{1+...}\)
- B2: Tìm thương và số dư của 24089 cho 6038, thương là 3, dư 5975, viết \(B=32+\frac{1}{1+\frac{1}{3+...}}\)
- B3: Tìm thương và số dư của 6038 cho 5975, thương là 1, dư 63, viết \(B=32+\frac{1}{1+\frac{1}{3+\frac{1}{1+...}}}\)
- B4: Tìm thương và số dư của 5975 cho 63, thương là 94, dư 53, viết \(B=32+\frac{1}{1+\frac{1}{3+\frac{1}{1+\frac{1}{94+...}}}}\)
...
Cứ làm như vậy, đến khi số dư là 1 thì dừng lại, phân số cuối cùng \(\frac{1}{b_n}\) thì bn chính là số chia cuối cùng, bn = 3
Kết quả: \(B=32+\frac{1}{1+\frac{1}{3+\frac{1}{1+\frac{1}{94+\frac{1}{1+\frac{1}{5+\frac{1}{3+\frac{1}{3}}}}}}}}\)

B A C F D H E
Kẻ đường cao AH của tam giác ABC. Ta có: SADEF = 2.2=4 => SABC = 9. Ta có :\(S_{ABC}=\frac{1}{2}.BC.AH=\frac{1}{2}.3\sqrt{5}.AH=9\Rightarrow AH=\frac{6}{\sqrt{5}}\).
Áp dụng ĐL Py-ta-go ta tính được \(AE=\sqrt{2^2+2^2}=2\sqrt{2}>\frac{6}{\sqrt{5}}\Rightarrow E\ne H\Rightarrow\)Tam giác AEH vuông tại H.
Ta có: \(\sin AEH=\frac{AH}{AE}=\frac{3}{\sqrt{10}}\Rightarrow AEH\approx71^034'\)=>Góc ECA = 180o-góc EAC-góc AEC = 180o - 45o - 71o34' = 63o26'
\(\Rightarrow\sin BCA=\sin63^026'=\frac{AB}{BC}\approx0,894\Rightarrow AB\approx6\left(cm\right)\). Vận dụng ĐL Py-ta-go ta có:
\(AC=\sqrt{BC^2-AB^2}=3\)

:v Làm bài 31 thôi nhá , còn lại all tự làm -..-
Gọi x (cm) , y (cm) là độ dài hai cạnh góc vuông của tam giác vuông (x > 2, y > 4).
Diện tích tam giác ban đầu là \(\frac{1}{2}xy\left(cm^2\right)\)
+ Tăng mỗi cạnh lên 3cm thì tam giác vuông mới có độ dài 2 cạnh là x + 3(cm) và y + 3 (cm)
Diện tích tam giác mới là : \(\frac{1}{2}\left(x+3\right)\left(y+3\right)\left(cm^2\right)\)
Diện tích tăng thêm 36 cm2 nên ta có p/trình :
\(\frac{1}{2}\left(x+3\right)\left(y+3\right)=\frac{1}{2}xy+36\)
\(\Leftrightarrow\left(x+3\right)\left(y+3\right)=xy+72\)
\(\Leftrightarrow xy+3x+3y+9=xy+72\)
\(\Leftrightarrow3x+3y=63\)
\(\Leftrightarrow x+y=21\)
+ Giảm một cạnh 2cm và giảm cạnh kia 4cm thì tam giác vuông mới có 2 cạnh là : x – 2 (cm) và y – 4 (cm).
Diện tích tam giác mới là : \(\frac{1}{2}\left(x-2\right)\left(y-4\right)\left(cm^2\right)\)
Diện tích giảm đi 26cm2 nên ta có phương trình :
\(\frac{1}{2}\left(x-2\right)\left(y-4\right)=\frac{1}{2}xy-26\)
\(\Leftrightarrow\left(x-2\right)\left(y-4\right)=xy-52\)
\(\Leftrightarrow xy-4x-2y+8=xy-52\)
\(\Leftrightarrow4x+2y=60\)
\(\Leftrightarrow2x+y=30\)
Ta có hệ phương trình : \(\hept{\begin{cases}x+y=21\\2x+y=30\end{cases}}\)
Lấy phương trình thứ hai trừ phương trình thứ nhất ta được :
\(\hept{\begin{cases}\left(2x+y\right)-\left(x+y\right)=30-21\\x+y=21\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2x+y-\left(x+y\right)=9\\x+y=21\end{cases}\Leftrightarrow\hept{\begin{cases}x=9\\y=12\end{cases}}}\)
Vậy tam giác có hai cạnh lần lượt là 9cm và 12cm
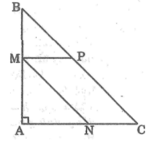




Gọi x (cm) là độ dài đoạn AM.
Điều kiện: 0 < x < 12
Vì ΔABC vuông cân tại A nên ΔBMP vuông cân tại M.
Suy ra MP = MB = AB – AM = 12 – x (cm)
Diện tích hình bình hành MNCP bằng MP.MA = (12 – x)x ( c m 2 )
Theo đề bài, ta có phương trình:
(12 – x)x = 32 ⇔ x 2 – 12x + 32 = 0
∆ ' = - 6 2 – 1.32 = 36 – 32 = 4 > 0
∆ ' = 4 = 2
Cả hai giá trị của x đều thỏa mãn điều kiện bài toán
Vậy điểm M cách điểm A 8cm hoặc 4cm thì diện tích hình bình hành MNCP bằng 32 c m 2