Cứu sắp hết giờ rồi 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(42\cdot102-43\cdot17-42\cdot34\)
\(=42\left(102-34\right)-43\cdot17\)
\(=168\cdot17-42\cdot17\)
\(=17\cdot126=2142\)
c: \(3\cdot42-22\cdot3=3\cdot20=60\)

\(A=\dfrac{3}{2\cdot2}=\dfrac{3}{4}\\ A=\dfrac{3}{2\cdot5}=\dfrac{3}{10}\\ A=\dfrac{3}{2\cdot3}=\dfrac{1}{2}\)


a) (23.37-11.37):37
=(23-11).37:37
=12.(37:37)
=12.1
=12
b)91.172+91.13-91.85
=91.(172+13-85)
=91.100
=9100
a, ( 23 × 37 - 11 × 37 ) ÷ 37
= 37 × ( 23 - 11 ) ÷ 37
= 37 × 12 ÷ 37
= 444 ÷ 37
= 12
b, 91 × 172 + 91 × 13 - 91 × 85
= 91 × ( 172 + 13 - 85 )
= 91 × 100
= 91000

Gọi các phân số cần tìm là: \(\dfrac{a}{b}\) theo bài ra ta có:
\(\dfrac{a}{b}\) = \(\dfrac{a+2}{b\times2}\)
a.(b x 2) = (a + 2) x b
ab x 2 = ab + 2b
ab = 2b
a = 2
Ta có: \(\dfrac{2}{b}\) > \(\dfrac{1}{5}\) = \(\dfrac{2}{10}\)
⇒ b < 10 ⇒ b = 1; 2; 3; 4; 5; 6; 7; 8; 9
Vì \(\dfrac{2}{b}\) không phải là số tự nhiên nên b \(\in\) {3; 4; 5; 6; 7; 8; 9}
Bài 16:
\(\dfrac{1}{6}\) < \(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\) + \(\dfrac{1}{7^2}\) +...+ \(\dfrac{1}{100^2}\) < \(\dfrac{1}{4}\)
\(\dfrac{1}{5^2}\) < \(\dfrac{1}{4.5}\) = \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\)
\(\dfrac{1}{6^2}\) < \(\dfrac{1}{5.6}\) = \(\dfrac{1}{5}\) - \(\dfrac{1}{6}\)
............................
\(\dfrac{1}{100^2}\) < \(\dfrac{1}{99.100}\) = \(\dfrac{1}{99}\) - \(\dfrac{1}{100}\)
Cộng vế với vế ta có:
\(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\)+...+ \(\dfrac{1}{100^2}\) < \(\dfrac{1}{4}\) - \(\dfrac{1}{100}\) < \(\dfrac{1}{4}\) (1)
\(\dfrac{1}{5^2}\) > \(\dfrac{1}{5.6}\) = \(\dfrac{1}{5}\) - \(\dfrac{1}{6}\)
\(\dfrac{1}{6^2}\) > \(\dfrac{1}{6.7}\) = \(\dfrac{1}{6}\) - \(\dfrac{1}{7}\)
...............................
\(\dfrac{1}{100^2}\) > \(\dfrac{1}{100.101}\) = \(\dfrac{1}{100}\) - \(\dfrac{1}{101}\)
Cộng vế với vế ta có:
\(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\) + ... + \(\dfrac{1}{100^2}\) > \(\dfrac{1}{5}\) - \(\dfrac{1}{101}\)= \(\dfrac{96}{505}\) > \(\dfrac{96}{576}\) = \(\dfrac{1}{6}\) (2)
Kết hợp (1) và (2) ta có:
\(\dfrac{1}{6}\) < \(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\) +...+ \(\dfrac{1}{100^2}\) < \(\dfrac{1}{4}\) (đpcm)

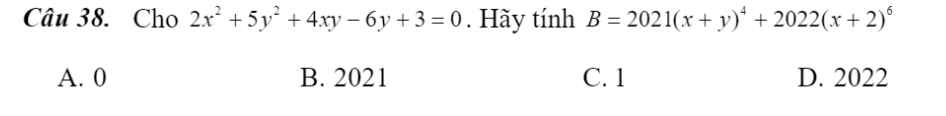


 cứu với mình sắp đi học rồi cứuuuu :(((((((
cứu với mình sắp đi học rồi cứuuuu :(((((((
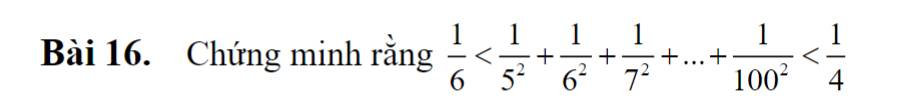 Cứu mình gấp ạ!!! Mình sắp thi rồi!!!
Cứu mình gấp ạ!!! Mình sắp thi rồi!!!