Cho hình chóp S.ABC có đáy ABC vuông tại B, SA vuông góc với đáy ABC. Khẳng định nào dưới đây sai?
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

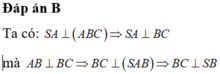

Đáp án B
Ta có: S A ⊥ A B C ⇒ S A ⊥ B C mà A B ⊥ B C ⇒ B C ⊥ S A B ⇒ B C ⊥ S B

Đáp án là B.
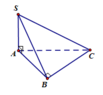
ta có S A ⊥ A B C ⇒ S A ⊥ A B S A ⊥ A C S A ⊥ B C Suy ra các phương án B, D đều đúng.
Ta có B C ⊥ S A B C ⊥ A B ⇒ B C ⊥ S B . Suy ra phương án C đúng
Ta có S ∉ A C S A ⊥ A C nên chỉ có đường thẳng SA vuông góc với AC . Do đó không tồn tại S B ⊥ A C . Phương án A sai.

Đáp án B.
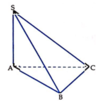
Ta có S A ⊥ ( A B C ) A B ⊂ ( A B C ) B C ⊂ ( A B C ) ⇒ S A ⊥ A B và S A ⊥ B C . Vậy A, C đúng.
Do Δ A B C vuông tại B nên B C ⊥ A B .
Ta có B C ⊥ S A , S A ⊂ S A B B C ⊥ A B , A B ⊂ S A B S A ∩ A B = A ⇒ B C ⊥ S A B , S B ⊂ S A B ⇒ B C ⊥ S B
Vậy B đúng.

Đáp án C
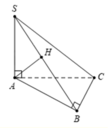
Tam giác ABC vuông tại B ⇒ A B ⊥ B C
Mà S A ⊥ A B C ⇒ S A ⊥ B C ⇒ B C ⊥ S A B ⇒ B C ⊥ S B
Và A H ⊥ B C mà A H ⊥ S B ⇒ A H ⊥ S B C ⇒ A H ⊥ B C A H ⊥ S C
Vậy hai đường thẳng S B , A C chéo nhau.