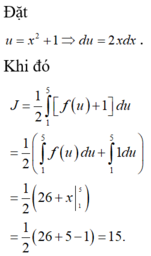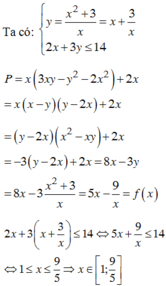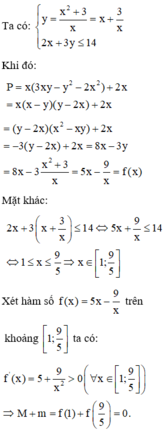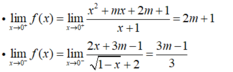\(\frac{X2+O2}{02X}\)=\(\frac{HOHO}{02X}\) ĐÂY LÀ CÔNG THỨC X2+02 =HÔHO
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 2 2018
Ta có:
x 2 - x y + 3 = 0 1 2 x + 3 y - 14 ≤ 0 2
Do x,y>0 nên ⇔ x 2 + 3 x thay vào (2) ta được:
2 x + 3 . x 2 + 3 x - 14 ≤ 0
⇔ 2 x 2 + 3 x 2 + 9 - 14 x x ≤ 0
⇔ 5 x 2 - 14 x + 9 ≤ 0 ⇔ 1 ≤ x ≤ 9 5
Thay y = x 2 + 3 x vào P ta được:
P = 3 x 2 y - x y 2 - 2 x 3 + 2 x
= 3 x 2 . x 2 + 3 x - x . x 2 + 3 x 2 - 2 x 3 + 2 x
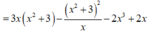
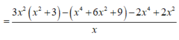
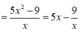
P ' = 5 + 9 x 2 > 0 với mọi x nên hàm số P=P(x) đồng biến trên 1 ; 9 5
Vậy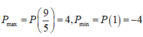 
Tổng 
.
Chọn đáp án B.
CM
9 tháng 3 2017
Đáp án B
Phương pháp:
- Rút y từ phương trình đầu, thay vào bất phương trình sau tìm điều kiện của x .
- Thay y ở trên vào biểu thức P đưa về biến x .
- Sử dụng phương pháp hàm số đánh giá P tìm GTLN, GTNN.
CM
11 tháng 4 2017
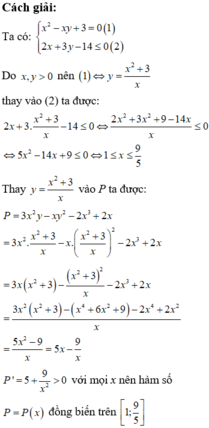
Đáp án B
Trên khoảng 0 ; + ∞ , ta có y ' = 2 x − 2 = 0 ⇒ x = 1 ⇒ Hàm số có 1 điểm cực trị.
Trên khoảng 1 ; 0 , ta có y ' = 2 > 0 ; ∀ x ∈ − 1 ; 0 ⇒ Hàm số đồng biến trên − 1 ; 0 .
Trên khoảng − ∞ ; − 1 , ta có y ' = − 3 < 0 ; ∀ x ∈ − ∞ ; − 1 ⇒ Hàm số nghịch biến trên − ∞ ; − 1 .
Vậy hàm số đã cho có một điểm cực trị.
CM
31 tháng 12 2019
Đáp án D
Ta có y = x 2 − 2 x khi x ≥ 0 2 x khi − 1 ≤ x < 0 − 3 x − 5 khi x < − 1 ⇒ y ' = 2 x − 2 khi x > 0 2 khi − 1 < x < 0 − 3 khi x < − 1
Dễ thấy y' đổi dấu khi qia các điểm x = 1 ; x = 0 ; x = − 1
CM
30 tháng 12 2019
- Ta có:
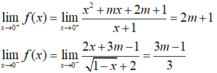
- Hàm số có giới hạn khi x → 0 khi và chỉ khi:
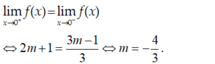
Chọn D.
