Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Leftrightarrow\dfrac{f'\left(x\right)}{f\left(x\right)}+2x=lnx\Rightarrow\dfrac{f'\left(x\right)}{f\left(x\right)}=lnx-2x\)
Lấy nguyên hàm 2 vế:
\(\Rightarrow\int\dfrac{f'\left(x\right)}{f\left(x\right)}dx=\int\left(lnx-2x\right)dx\)
\(\Rightarrow ln\left|f\left(x\right)\right|=x\left(lnx-1\right)-x^2+C\)
Thay \(x=1\)
\(\Rightarrow ln\left|f\left(1\right)\right|=-2+C\Rightarrow C=2\)
\(\Rightarrow ln\left|f\left(x\right)\right|=x\left(lnx-1\right)-x^2+2\)
\(\Rightarrow\left|f\left(x\right)\right|=e^{x\left(lnx-1\right)-x^2+2}\)
\(\Rightarrow\left|f\left(2\right)\right|\)

Đề là cho \(\int\limits^{\dfrac{\pi}{2}}_0sin2x.f\left(cos^2x\right)dx=1\)
Tính \(\int\limits^1_0\left[2f\left(1-x\right)-3x^2+5\right]dx\)
Đúng ko nhỉ?
Xét \(\int\limits^{\dfrac{\pi}{2}}_0sin2x.f\left(cos^2x\right)dx\)
Đặt \(cos^2x=1-u\Rightarrow-2sinx.cosxdx=-du\) \(\Rightarrow sin2xdx=du\)
\(\left\{{}\begin{matrix}x=0\Rightarrow u=0\\x=\dfrac{\pi}{2}\Rightarrow u=1\end{matrix}\right.\) \(\Rightarrow I=\int\limits^1_0f\left(1-u\right)du=\int\limits^1_0f\left(1-x\right)dx\)
\(\Rightarrow\int\limits^1_0f\left(1-x\right)dx=1\)
\(\Rightarrow\int\limits^1_0\left[2f\left(1-x\right)-3x^2+5\right]dx=2\int\limits^1_0f\left(1-x\right)dx-\int\limits^1_0\left(3x^2-5\right)dx\)
\(=2.1-\left(-4\right)=6\)

\(f\left(0\right)=\dfrac{b}{d}\Rightarrow f\left(f\left(0\right)\right)=0\Rightarrow f\left(\dfrac{b}{d}\right)=0\)
\(\Rightarrow\dfrac{\dfrac{ab}{d}+b}{\dfrac{cb}{d}+d}=0\Rightarrow b\left(a+d\right)=0\Rightarrow\left[{}\begin{matrix}b=0\\d=-a\end{matrix}\right.\)
TH1: \(b=0\)
\(f\left(1\right)=1\Rightarrow a=c+d\)
\(f\left(2\right)=2\Rightarrow2a=2\left(2c+d\right)\Rightarrow a=2c+d\)
\(\Rightarrow2c+d=c+d\Rightarrow c=0\) (ktm)
TH2: \(d=-a\)
\(f\left(1\right)=1\Rightarrow a+b=c+d=c-a\Rightarrow2a+b=c\) (1)
\(f\left(2\right)=2\Rightarrow2a+b=2\left(2c+d\right)=2\left(2c-a\right)\Rightarrow4a+b=4c\) (2)
Trừ (2) cho (1) \(\Rightarrow2a=3c\Rightarrow\dfrac{a}{c}=\dfrac{3}{2}\)
\(\Rightarrow\lim\limits_{x\rightarrow\infty}\dfrac{ax+b}{cx+d}=\dfrac{a}{c}=\dfrac{3}{2}\)
Hay \(y=\dfrac{3}{2}\) là tiệm cận ngang
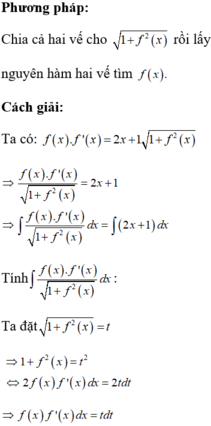
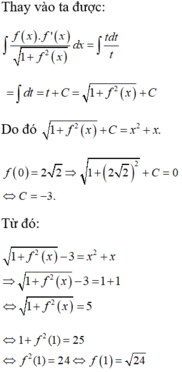
Đáp án D.