Có bao nhiêu số tự nhiên có bốn chữ số khác nhau được tạo thành từ các chữ số của tập X = 1 , 3 , 5 , 8 , 9 .
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn đáp án D
Phương pháp
Sử dụng công thức chỉnh hợp.
Cách giải
Số các số tự nhiên có 4 chữ số khác nhau được tạo thành từ X={1;3;5;8;9} là A 5 4 số

Chọn D
*) Ta có: ![]()
*) Tính n(A): Giả sử 8 chữ số được viết vào 8 ô trống được đánh số từ 1 đến 8
TH1: Xếp bất kỳ
Xếp hai chữ số 1, hai chữ số 2 và 4 chữ số còn lại: Có ![]() (cách).
(cách).
TH2: Số các cách xếp sao cho không thỏa mãn yêu cầu bài toán
Xếp hai chữ số 1 đứng liền nhau: Có ![]() cách.
cách.
Xếp hai chữ số 2 đứng liền nhau: Có ![]() cách.
cách.
Số các cách xếp thuộc cả hai trường hợp trên:
+ Coi hai chữ số 1đứng liền nhau là nhóm X, hai chữ số 2 đứng liền nhau là nhóm Y
+ Xếp X, Y và 4 số còn lại có: ![]() (cách)
(cách)
Vậy số cách xếp không thỏa mãn yêu cầu là: ![]() (cách)
(cách)
Vậy ![]()
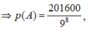

ĐÙ Ù Ù Ù Ù CHUẨN VẢI NỒI ??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? ĐỈNH CỦA CHỚP LUÔN VỘ TAY VỘ TAY

Các số có 4 chữ số có dạng: \(\overline{abcd}\)
Trong đó
\(a\) có 3 cách chọn
\(b\) có 3 cách chọn
\(c\) có 2 cách chọn
\(d\) có 1 cách chọn
Số các số có 4 chữ số khác nhau được lập từ 4 chữ số đã cho là:
3 \(\times\) 3 \(\times\) 2 \(\times\) 1 = 18 (số)
Vậy tập Y có 18 phần tử