Cho hình lập phương ABCD. A'B'C'D' cạnh bằng a. Góc giữa B'D và mặt phẳng (AA'D'D) gần nhất với góc nào sau đây?
A. 20 o
B. 35 o
C. 45 o
D. 60 o
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
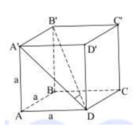

=> A' là hình chiếu vuông góc của B' trên (AA'D'D)
=> A'D là hình chiếu vuông góc của B'D trên (AA'D'D)


Đáp án D
Gọi I là giao điểm của AC và BD
A I ⊥ B D A I ⊥ B B ' ⇒ A I ⊥ B B ' D ' D
=> B’I là hình chiếu vuông góc của AB’ lên (BB’D’D)
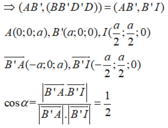


b) Ta có ACC' là tam giác vuông có cạnh \(AC=a\sqrt{2},CC'=a\)
Vậy \(AC'^2=AC^2+CC^2\Rightarrow AC'^2=2a^2+a^2=3a^2\)
Vậy \(AC'=a\sqrt{3}\)

Đáp án D
Diện tích toàn phần của hình lập phương cạnh a là S t p = 6 a 2 .
Khi dùng các mặt phẳng như đề bài cho để chia khối lập phương ABCD.A’B’C’D’ ta được 125 khối lập phương nhỏ bằng nhau.
Do đó diện tích toàn phần của 1 khối lập phương nhỏ là 480 125 = 96 25
Gọi cạnh hình lập phương ABCD.A’B’C’D’ bằng a thì độ dài cạnh hình lập phương nhỏ bằng a 5 .
Suy ra diện tích toàn phần của 1 hình lập phương nhỏ là: 6 a 5 2 = 96 25 ⇔ a = 4

Đáp án D
Phương pháp: - Cách xác định góc giữa hai mặt phẳng:
Gọi a’ là hình chiếu vuông góc của a trên mặt phẳng (P).
Góc giữa đường thẳng a và mặt phẳng (P) là góc giữa đường thẳng a và a’.
Cách giải:
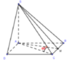
Vì ![]()
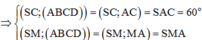
ABCD là hình chữ nhật ![]()
∆SAC vuông tại A ![]()
![]()
∆ABM vuông tại B ![]()
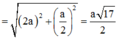
∆SAM vuông tại A 

![]()
Đáp án B