Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.có 18 HLP nhỏ có mặt được sơn xanh,1 HLP nhỏ có 1 mặt sơn xanh
b.có 24 HLP nhỏ được sơn đỏ ,có 12 HLP nhỏ đc sơn đỏ 2 mặt,12 HLP nhỏ đc sơn đỏ 1 mặt
c. có 3 HLP nhỏ không đc sơn mặt nào
tích mình nhé :D thanks

Câu 1:
\(AB=\sqrt{\left[3-\left(-2\right)\right]^2+\left(3-2\right)^2}=\sqrt{26}\)
\(BC=\sqrt{\left(2-3\right)^2+\left(-2-3\right)^2}=\sqrt{26}\)
\(AC=\sqrt{\left[2-\left(-2\right)\right]^2+\left(-2-2\right)^2}=4\sqrt{2}\)
\(P=\dfrac{AB+BC+AC}{2}=\dfrac{2\sqrt{26}+4\sqrt{2}}{2}=\sqrt{26}+2\sqrt{2}\)
\(S=\sqrt{\left(\sqrt{26}+2\sqrt{2}\right)\cdot2\sqrt{2}\cdot2\sqrt{2}\cdot\left(\sqrt{26}-2\sqrt{2}\right)}=\sqrt{18\cdot8}=12\left(đvdt\right)\)

Lời giải:
a) Gọi phương trình đường thẳng có dạng $y=ax+b$ $(d)$
Vì \(B,C\in (d)\Rightarrow \left\{\begin{matrix} 3=2a+b\\ -3=-4a+b\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=1\\ b=1\end{matrix}\right.\Rightarrow y=x+1\)
Vậy PT đường thẳng chứa cạnh $BC$ có dạng $y=x+1$
b) Tương tự, ta lập được phương trình đường thẳng chứa cạnh $AC$ là \((d_1):y=\frac{2x}{5}-\frac{7}{5}\).
Gọi PT đường cao đi qua $B$ của tam giác $ABC$ là \((d'):y=ax+b\)
Vì \((d')\perp (d_1)\Rightarrow \frac{2}{5}a=-1\Rightarrow a=\frac{-5}{2}\).
Mặt khác \(B\in (d')\Rightarrow 3=\frac{-5}{2}.2+b\Rightarrow b=8\)
\(\Rightarrow (d'):y=\frac{-5x}{2}+8\)
c) Gọi điểm thỏa mãn ĐKĐB là $M(a,b)$
Ta có: \(M\in (\Delta)\Rightarrow 2a+b-3=0\) $(1)$
$M$ cách đều $A,B$ \(\Rightarrow MA^2=MB^2\Rightarrow (a-1)^2+(b+1)^2=(a-2)^2+(b-3)^2\)
\(\Leftrightarrow 2-2a+2b=13-4a-6b\)
\(\Leftrightarrow 11-2a-8b=0(2)\)
Từ \((1);(2)\Rightarrow \left\{\begin{matrix} a=\frac{13}{14}\\ b=\frac{8}{7}\end{matrix}\right.\Rightarrow M\left ( \frac{13}{14};\frac{8}{7} \right )\)
con nếu đề bài cho 1 điểm và phương trình đường thẳng của tam giác muốn tìm phương trình đường cao còn lại vầ các cạnh thj làm thế nào

Chia lăng trụ ABD.A'B'D' thành ba tứ diện DABD', A'ABD', A'B'BD'. Phép đối xứng qua (ABD') biến DABD' thành A'ABD', Phép đối xứng qua (BA'D') biến A'ABD' thành A'B'BD' nên ba tứ diện DABA', A'ABD', A'B'BD' bằng nhau
Làm tương tự đối với lăng trụ BCD.B'C'D' ta sẽ chia được hình lập phương thành sáu tứ diện bằng nhau.

Đáp án C
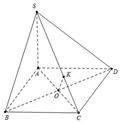
Gọi O là tâm hình vuông ABCD ta có:
A C ⊥ B D B D ⊥ S A ⇒ B D ⊥ S A C
Dựng O K ⊥ S C ⇒ O K là đoạn vuông góc chung của BD và SC
Khi đó d B D ; S C = O K = 1 2 d A ; S C = 1 2 S A . A C S A 2 + A C 2
Với A C = a 2 ⇒ d = a 6 6 .

a: Gọi mẫu là x
Theo đề, ta có:
\(\dfrac{2}{5}< \dfrac{4}{x}< \dfrac{2}{3}\)
=>10>x>6
=>\(x\in\left\{9;8;7\right\}\)
b: Phần phân số là 1-9/25=16/25
Phần nguyên là 125x9/25=45
Vậy: Hỗn số cần tìm là \(45\dfrac{16}{25}\)
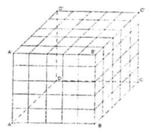
Đáp án D
Diện tích toàn phần của hình lập phương cạnh a là S t p = 6 a 2 .
Khi dùng các mặt phẳng như đề bài cho để chia khối lập phương ABCD.A’B’C’D’ ta được 125 khối lập phương nhỏ bằng nhau.
Do đó diện tích toàn phần của 1 khối lập phương nhỏ là 480 125 = 96 25
Gọi cạnh hình lập phương ABCD.A’B’C’D’ bằng a thì độ dài cạnh hình lập phương nhỏ bằng a 5 .
Suy ra diện tích toàn phần của 1 hình lập phương nhỏ là: 6 a 5 2 = 96 25 ⇔ a = 4