Cho hình chóp tứ giác đều S.ABCD, cạnh đáy AB = 2a, góc A S B ⏜ = 2 α ( 0 ∘ < α < 90 ∘ ) . Gọi V là thể tích của khối chóp. Kết quả nào sau đây sai?
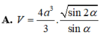
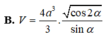
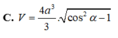
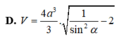
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Diện tích đáy S = 4 a 2
c o t 2 α + 1 = 1 sin 2 α ⇒ c o t 2 α - 1 = 1 sin 2 α - 2
Do đó (C) và (D) đúng
Từ câu (D) suy ra V = 4 a 3 3 . 1 - sin 2 α sin 2 α = 4 a 3 3 . cos 2 α sin α . Do đó (B) đúng
Vậy (A) là kết quả sai
Đáp án A

Đáp án C
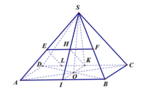
Ta có, CD song song mặt phẳng (SAB) chứa SA nên khoảng cách giữa SA và CD chính là khoảng cách từ CD đến (SAB).
Gọi I, K theo thứ tự là trung điểm AB, CD thì:

Trong đó H là hình chiếu từ K lên SI

Đáp án C
Ta có, CD song song mặt phẳng (SAB) chứa SA nên khoảng cách giữa SA và CD chính là khoảng cách từ CD đến (SAB).
Gọi I, K theo thứ tự là trung điểm AB, CD thì:
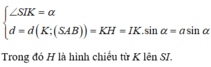

Đáp án A.
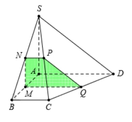
Gọi N, Q lần lượt là trung điểm của AB, CD ⇒ M N ⊥ A B M Q ⊥ A B .
Qua N kẻ đường thẳng song song với BC, cắt SC tại P.
Suy ra thiết diện của mặt phẳng α và hình chóp là MNPQ.
Vì MQ là đường trung bình của hình tháng ABCD ⇒ M Q = 3 a 2 .
MN là đường trung bình của tam giác SAB ⇒ M N = S A 2 = a .
NP là đường trung bình của tam giác SBC ⇒ N P = B C 2 = a 2 .
Vậy diện tích hình thang MNPQ là S M N P Q = M N . N P + M Q 2 = a 2 a 2 + 3 a 2 = a 2 .

Đáp án A
Đặt a> 0 cạnh hình vuông là Dễ thấy
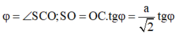
Gọi O là tâm của đáy. Vẽ AH ⊥ SC tại, H, AH cắt SO tại I thì A I O ^ = φ
![]()
Qua I vẽ đường thẳng song song DB cắt SD, SB theo thứ tự tại K, L. Thiết diện chính là tứ giác
ALHK và tứ giác này có hai đường chéo AH ⊥ KL Suy ra
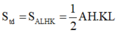
Ta có:


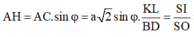
![]()
Theo giả thiết
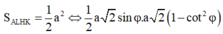
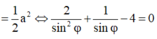
Giải được
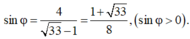
Suy ra φ = a r c sin 33 + 1 8

Phương pháp:
Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và vuông góc với giao tuyến.
Cách giải:
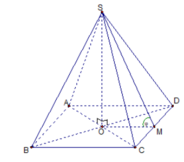
S . ABCD là chóp tứ giác đều cạnh bên SA = SB = SC = SD = 2a . Gọi O
là giao của AC và BD => SO ⊥ (ABCD)
Gọi H là trung điểm CD => SH ⊥ CD
Mà ABCD là hình vuông nên OC = OD => OH ⊥ CD
Ta có 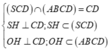
=> góc giữa mặt đáy (ABCD) và mặt bên (SCD) là SHO
Ta có OH là đường trung bình của ![]()
Xét tam giác SHC, theo định lý Pytago ta có
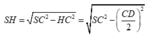
![]()
Xét tam giác SOH vuông tại S (do SO ⊥ (ABCD))
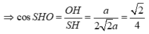
Chọn A.
Đáp án A