Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
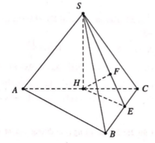
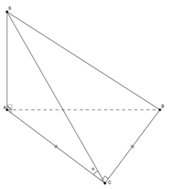
Dựng SH ⊥ AC , do ( SAC ) ⊥ ( ABC ) nên SH ⊥ ( ABC ) ; AC = 2 a . Dựng HE ⊥ BC ; HF ⊥ SE ⇒ d ( H ; ( SBC ) ) = HF . ΔSAC = ΔBCA ⇒ ΔSAC vuông tại S .
Dễ thấy tan ACB ^ = 1 3 ⇒ ACB ^ = 30 o = SAC ^ HC = SCcos 60 o = a 2 ; HE = HCsin 30 o = a 4 ; SH = a 3 2 . Do AC = 4 HC ⇒ d A = 4 d H = 4 . SH . HE SH 2 + HE 2 = 2 39 13 Do đó Sinα = d A SA = 2 13 .

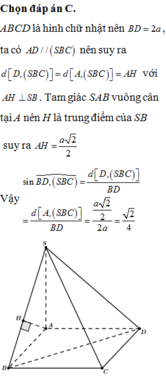
Đáp án C
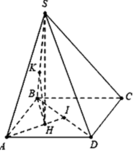
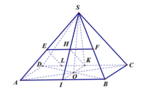
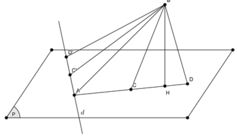
Gọi H là tâm đường tròn ngoại tiếp đều ∆ABD
Ta có 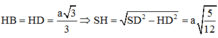
Lại có d(H;(SBC)) = HK và 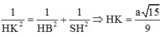
Khoảng cách từ D →(SBC) là 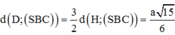
Vậy ∆ABD ![]()

Đáp án C
Ta có, CD song song mặt phẳng (SAB) chứa SA nên khoảng cách giữa SA và CD chính là khoảng cách từ CD đến (SAB).
Gọi I, K theo thứ tự là trung điểm AB, CD thì:
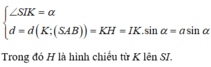

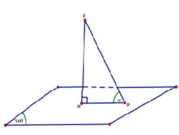




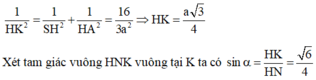
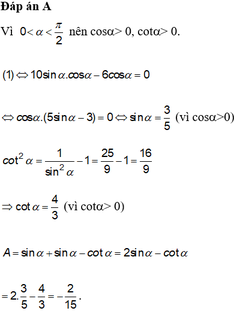


Diện tích đáy S = 4 a 2
c o t 2 α + 1 = 1 sin 2 α ⇒ c o t 2 α - 1 = 1 sin 2 α - 2
Do đó (C) và (D) đúng
Từ câu (D) suy ra V = 4 a 3 3 . 1 - sin 2 α sin 2 α = 4 a 3 3 . cos 2 α sin α . Do đó (B) đúng
Vậy (A) là kết quả sai
Đáp án A