Cho khối lăng trụ tam giác đều A B C . A 1 B 1 C 1 có tất cả các cạnh bằng a. Gọi M là trung điểm của A A 1 . Thể tích khối chóp M . B C A 1 là:

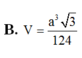
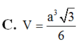
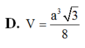
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Để ý rằng hai khối lăng trụ đó có diện tích đáy bằng nhau, tỉ số hai đường cao tương ứng bằng 1/2.
a.1/2
okkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkk

Gọi O là trung điểm cạnh
A
B
⇒
A
'
O
⊥
A
B
C
và ![]()
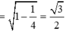
Vì vậy ![]()
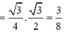
Chọn đáp án B.

Đáp án D
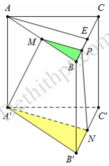
Gọi E là trung điểm của BC, F là trung điểm của BE
Khi đó M F / / A E mà A E / / A ' N nên M F / / A ' N
Suy ra các điểm A ' , M , F , N thuộc cùng một mặt phẳng
Vậy A ' M N cắt cạnh BC tại P ⇒ P trùng với F
Công thức tổng quát tính thể tích khối đa diện
“thể tích khối chóp cụt là V = h 3 B + B ' + B B ' với h là chiều cao, B, B’ lần lượt là diện tích hai đáy”
Và diện tích đáy B = S M B P = S A B C 8 = S 8 B ' = S A ' B ' N = S A ' B ' C ' 2 = S 2 với S = a 2 3 4
⇒ Thể tích khối đa diện M N P . A ' B ' N là V = B B ' 3 S 8 + S 2 + S 8 . S 2 = 7 3 a 3 96
Đáp án B