Cho hai chất điểm A và B cùng bắt đầu chuyển động trên trục Ox từ thời điểm t = 0. Tại thời điểm t, vị trí chất điểm A được cho bởi x = f t = − 6 + 2 t − 1 2 t 2 và vị trí của chất điểm B được cho bởi x = g t = 4 sin t . Biết tại đúng hai thời điểm t 1 và t 2 t 1 < t 2 , hai chất điểm có vận tốc bằng nhau. Tính theo t 1 và t 2 độ dài quãng đường mà chất điểm A đã di chuyển từ thời điểm t 1 đến thời điểm t 2 .
A. 4 − 2 t 1 + t 2 + 1 2 t 1 2 + t 2 2
B. 4 + 2 t 1 + t 2 − 1 2 t 1 2 + t 2 2
C. 2 t 2 − t 1 − 1 2 t 2 2 − t 1 2
D. 2 t 1 − t 2 − 1 2 t 1 2 − t 2 2







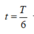
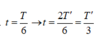
Đáp án A
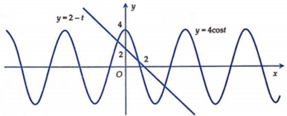
Cách 1: Ta có f ' t = 2 − t ; g ' t = 4 cos t
Vẽ đồ thị hàm số y = f ' t và y = g ' t ta có
Nhìn vào đồ thị ta thấy 0 < t 1 < t 2 f ' t 1 > 0 f ' t 2 < 0 f 2 = 0 và f 2 = − 6 + 4 − 2 = − 4 f t 1 = − 6 + 2 t 1 − 1 2 t 1 2 f t 2 = − 6 + 2 t 2 − 1 2 t 2 2
⇒ s = f 2 − f t 1 + f 2 − f t 2 = − 4 − − 6 + 2 t 1 − 1 2 t 1 2 + − 4 − − 6 + 2 t 2 − 1 2 t 2 2
= 4 + 1 2 t 1 2 + t 2 2 − 2 t 1 + t 2
Sử dụng tích phân
Từ cách 1 ta có hai chất điểm gặp nhau khi 2 − t = 4 cos t ⇔ t 1 = A t 2 = B
Từ hình vẽ ở cách 1 ta có A < 2 < B
Quãng đường đi được từ thời điểm A đến thời điểm B được tính bằng công thức
∫ A B 2 − t d t = ∫ A 2 2 − t d t + ∫ 2 B 2 − t d t = ∫ A 2 2 − t d t + ∫ 2 B t − 2 d t
= 2 t − t 2 2 2 A + t 2 2 − 2 t B 2
= 4 − 2 − 2 A + A 2 2 + B 2 2 − 2 B − 2 + 4
= 4 + 1 2 A 2 + B 2 − 2 A + B = 4 + 1 2 t 1 2 + t 2 2 − 2 t 1 + t 2