Cho hình lăng trụ ABC.A’B’C’ có tất cả các cạnh cùng bằng a, hình chiếu của C trên mặt phẳng (ABB’A’) là tâm của hình bình hành ABB’A’. Tính theo a thể tích khối cầu đi qua năm điểm A, B, B’, A’ và C. A.
π
2
a
3
3
B.
8
π
2
a
3
81
C.
π
2
a
3
24
D.
π
2
a
3
...
Đọc tiếp
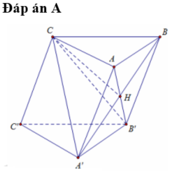
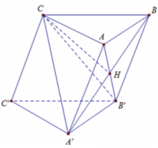
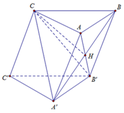
Cho hình lăng trụ ABC.A’B’C’ có tất cả các cạnh cùng bằng a, hình chiếu của C trên mặt phẳng (ABB’A’) là tâm của hình bình hành ABB’A’. Tính theo a thể tích khối cầu đi qua năm điểm A, B, B’, A’ và C.
A. π 2 a 3 3
B. 8 π 2 a 3 81
C. π 2 a 3 24
D. π 2 a 3 81
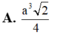
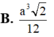
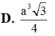
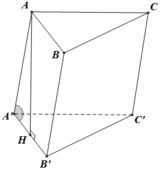
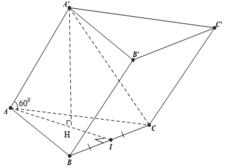
Đáp án A
Gọi O là tâm hình bình hành A B B ' A ' , ta có C O ⊥ A B B ' A ' .
Vì C A = C B nên O A = O B , suy ra hình thoi A B B ' A ' là hình vuông.
Do đó O A = A B 2 = a 2 . Suy ra O C 2 = A C 2 − A O 2 = a 2 2 ⇒ O C = a 2
Suy ra tam giác ABC vuông tại C. Từ đây ra suy ra khối caauff đi qua năm điểm A ; B ; B ' ; A ' và C là khối cầu tâm O bán kính O A = a 2 .
Vậy thể tích khối cầu là V = 4 3 π . O A 3 = π 2 a 3 3