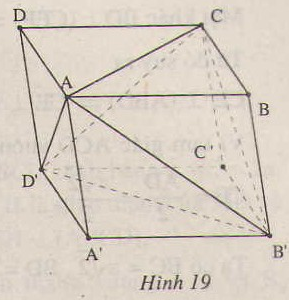
Cho hình hộp ABCD. A’B’C’D’ Tính tỉ số thể tích của khối tứ diện A’C’BD và khối hộp đã cho
A. 1 3
B. 1 6
C. 1 2
D. 1 4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
26 tháng 1 2017
Đúng(0)
Những câu hỏi liên quan
CM
19 tháng 7 2017
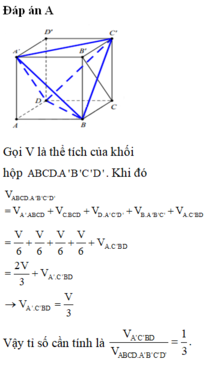
Đáp án A
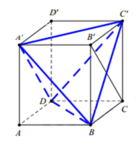
Gọi V là thể tích của khối hộp A B C D . A ' B ' C ' D ' . Khi đó
V A B C D . A ' B ' C ' D ' = V A ' . A B C D + V C . B C D + V D . A ' C ' D ' + V B . A ' B ' C ' + V A . C ' B D
= V 6 + V 6 + V 6 + V 6 + V A . C ' B D = 2 V 3 + V A ' . C ' B D → V A ' . C ' B D = V 3
Vậy tỉ số cần tính là V A ' C ' B D V A B C D . A ' B ' C ' D ' = 1 3 .
CM
24 tháng 8 2017
Đáp án B
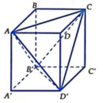
Nhìn hình vẽ ta thấy sẽ khó tính trực tiếp thể tích của khối tứ diện A C B ' D ' , do vậy ta sẽ tính gián tiếp.
Ta tính thể tích các khối tứ diện A C D D ' ; A A ' D ' B ' ; A B C B ' ; C C ; B ' D ' . Sau đó lấy thể tích khối hộp trừ đi tổng thể tích các khối trên.
Ta nhận thấy cả bốn khối tự diện A C D D ' ; A A ' D ' B ' ; A B C B ' ; C C ; B ' D ' đều có thể tích bằng nhau và bằng V 1 = 1 3 A A ' . 1 2 S A B C D = 1 6 V A B C D . A ' B ' C ' D ' = 1 6 V
Thể tích của khối tứ diện A C B ' D ' bằng V 2 = V − 4 6 V = V 3
Tỉ số cần tìm là 3. Ta chọn B
CM
25 tháng 5 2019
Phương pháp:
Phân chia khối hộp ra các phần, lập tỉ số thể tích.
Cách giải:
Gọi V là thể tích khối hộp ABCD.A'B'C'D'
Ta có: 
= 1 6 V
Mà 
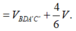
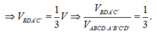
Chọn: C
SG
1
1 tháng 4 2017
Gọi S là diện tích đáy ABCD và h là chiều cao của khối hộp. Chia khối hộp thành khối tứ diện ACB’D’ và bốn khối chóp A.A’B’D’, C.C’B’D’, B’.BAC và D’. DAC. Ta thấy bốn khối chóp sau đều có diện tích đáy bằng và chiều cao bằng h, nên tổng các thể tích của chúng bằng
.
Từ đó suy ra thể tích của khối tứ diện
ACB’D’=. Do đó tỉ số của thể tích khối hộp đó và thể tích của khối tứ diện ACB’D’ bằng 3.
