Cho hàm số y = 3 x + 2 x 2 - 4 x + m có đồ thị C m .Mệnh đề nào sau đây sai?
A. C m có một tiềm cận ngang và hai tiệm cận đứng nếu m < 4
B. C m có một tiềm cận ngang và hai tiệm cận đứng nếu m = 4
C. C m luôn có hai tiệm cận đứng với mọi m
D. C m chỉ có một tiệm cận ngang nếu m > 4


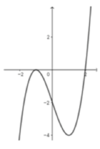
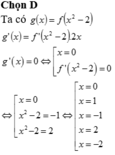

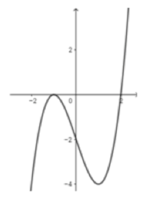
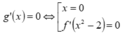
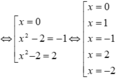
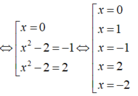


Ta có lim x → ± ∞ y = 0 ⇒ y = 0 là tiệm cận ngang của C m
Xét tam thức bậc hai f x = x 2 - 4 x + m . Nếu ∆ = 4 - m > 0 ⇔ m = 4 thì f(x) có hai nghiệm x 1 , x 2 phân biệt.
Do lim x → x 1 y = lim x → x 2 y = ± ∞ ⇒ C m có hai tiềm cận đứng
Đáp án C