Phát biểu thành lời các mệnh đề sau và xét tính đúng sai của chúng. ∃ x ∈ R : x 2 + x + 1 > 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
1 tháng 1 2019
Bình phương của mọi số thực đều nhỏ hơn hoặc bằng 0 (mệnh đề sai).
PT
1
CM
16 tháng 11 2019
Có một số thực mà bình phương của nó nhỏ hơn hoặc bằng 0 (mệnh đề đúng).
PT
1
CM
3 tháng 1 2017
Bình phương của mọi số thực đều dương.
– Mệnh đề này sai vì nếu x = 0 thì x2 = 0.
Sửa cho đúng: ∀ x ∈ R : x2 ≥ 0.
PT
1
CM
26 tháng 12 2017
Tồn tại số thực nhỏ hơn nghịch đảo của chính nó.
– Mệnh đề này đúng. Ví dụ 0,5 < 1/ 0,5.
AH
Akai Haruma
Giáo viên
8 tháng 9 2021
Lời giải:
a. Mệnh đề sai, vì $x^2\geq 0>-1$ với mọi $x\in\mathbb{R}$ theo tính chất bình phương 1 sosos.
Mệnh đề phủ định: $\forall x\in\mathbb{R}, x^2\neq -1$
b. Mệnh đề đúng, vì $x^2+x+2=(x+0,5)^2+1,75>0$ với mọi $x\in\mathbb{R}$ nên $x^2+x+2\neq 0$ với mọi $x\in\mathbb{R}$
Mệnh đề phủ định: $\exists x\in\mathbb{R}| x^2+x+2=0$
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Phát biểu: “Với mọi số thực, tổng của bình phương của nó và 1 luôn nhỏ hơn hoặc bằng 0”
Mệnh đề này sai, vì \(\forall x \in :{x^2} \ge 0\; \Rightarrow {x^2} + 1 \ge 1 > 0\)
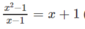
Có một số thực x, mà x 2 + x + 1 > 0 (mệnh đề đúng).