Tìm tọa độ tâm đối xứng của đồ thị hàm số y = 2 x + 1 x - 1 .
A. (1;2)
B. (2;1)
C. (1;-1)
D. (-1;1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 2 2017
Chọn B.
Tâm đối xứng của đồ thị hàm số này là giao điểm của 2 đường tiệm cận 1 2 ; 1 2
CM
1 tháng 8 2017
Đáp án B.
y' = 3x2 + 6x – 9
y’’ = 6x + 6
y’’ = 0 ó x = -1.
Thay x = -1 vào hàm số y = 12
CM
21 tháng 2 2017
Đáp án là D.
• Đồ thị có tiệm cận đứng và tiệm cận ngang làn lượt là: x = - 1 2 ; y = 3 2
• Giao điểm hai đường tiệm cận là tâm đối xứng của đồ thị hàm số.
CM
16 tháng 11 2019
Đáp án A
Phương pháp: Tham số hóa điểm thuộc đồ thị hàm số (C).
Lấy điểm đối xứng với điểm đó qua O (Điểm (a;) đối xứng với điểm (-a;-b)qua gốc tọa độ O).
Cho điểm đối xứng vừa xác định thuộc (C).
Cách giải:
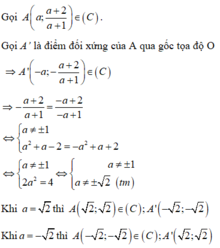
Chú ý và sai lầm : Có thể thử trực tiếp từng đáp án và suy ra kết quả.
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Tập giá trị của hàm số\(y = \sin x\) là \(\left[ { - 1;1} \right]\)
b) Đồ thị hàm số \(y = \sin x\) nhận O là tâm đối xứng.
Như vậy hàm số \(y = \sin x\) là hàm số lẻ.
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) song song với trục hoành sang phải theo đoạn có độ dài \(2\pi \), ta nhận được đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ {\pi ;3\pi } \right]\)
Như vậy, hàm số \(y = \sin x\) có tuần hoàn .
d) Hàm số \(y = \sin x\) đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\), nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\) với \(k \in Z\)
Chọn A