Có bao nhiêu giá trị nguyên của tham số m để phương trình m + 3 m + 3 cosx 3 3 = cosx có nghiệm thực
A. 5
B. 7
C. 3
D. 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

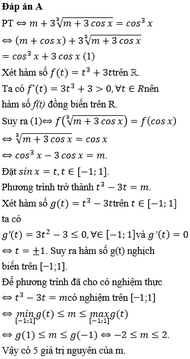

1.
\(3cos2x-7=2m\)
\(\Leftrightarrow cos2x=\dfrac{2m-7}{3}\)
Phương trình đã cho có nghiệm khi:
\(-1\le\dfrac{2m-7}{3}\le1\)
\(\Leftrightarrow2\le m\le5\)
2.
\(2cos^2x-\sqrt{3}cosx=0\)
\(\Leftrightarrow cosx\left(2cosx-\sqrt{3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=\pm\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\) Có 4 nghiệm \(\dfrac{\pi}{2};\dfrac{3\pi}{2};\dfrac{\pi}{6};\dfrac{11\pi}{6}\) thuộc đoạn \(\left[0;2\pi\right]\)

Đặt t = sin x + cos x − 2 ≤ t ≤ 2 ⇒ sin x cos x = t 2 − 1 2 .
Phương trình trở thành t 2 − 1 2 − t + m = 0 ⇔ − 2 m = t 2 − 2 t − 1 ⇔ t − 1 2 = − 2 m + 2 .
Do − 2 ≤ t ≤ 2 ⇒ − 2 − 1 ≤ t − 1 ≤ 2 − 1 ⇔ 0 ≤ t − 1 2 ≤ 3 + 2 2 .
Vậy để phương trình có nghiệm
⇔ 0 ≤ − 2 m + 2 ≤ 3 + 2 2 ⇔ − 1 + 2 2 2 ≤ m ≤ 1 → m ∈ ℤ m ∈ − 1 ; 0 ; 1 .
Chọn đáp án C.

\(m+3\sqrt[3]{m+3cosx}=cos^3x\)
Đặt \(\sqrt[3]{m+3cosx}=t\Rightarrow m=t^3-3cosx\)
\(\Rightarrow t^3-3cosx+3t=cos^3x\)
\(\Leftrightarrow t^3+3t=cos^3x+3cosx\)
Hàm \(f\left(t\right)=t^3+3t\) có \(f'\left(t\right)=3t^2+3>0\Rightarrow f\left(t\right)\) đồng biến
\(\Rightarrow t=cosx\) (hoặc là bạn liên hợp cũng được, tùy thích)
\(\Leftrightarrow m=t^3-3cosx=cos^3x-3cosx\)
Đặt \(cosx=u\in\left[-1;1\right]\Rightarrow f\left(u\right)=u^3-3u=m\)
Xét hàm \(f\left(u\right)=u^3-3u\) trên \(\left[-1;1\right]\)
\(f'\left(u\right)=3u^2-3\Rightarrow u=\pm1\)
\(f\left(-1\right)=2\) ; \(f\left(1\right)=-2\Rightarrow-2\le f\left(u\right)\le2\)
\(\Rightarrow-2\le m\le2\)

Đáp án B
Phương pháp:
Sử dụng phương pháp hàm số để giải phương trình.
Cách giải :
s inx 2019 − cos 2 x 2018 − cos x + m 2019 − sin 2 x + m 2 + 2 m cos x 2018 = cos x − s inx + m
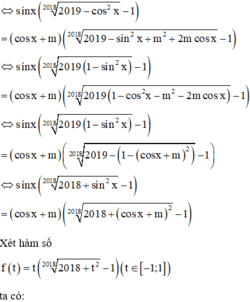
f ' t = 2018 + t 2 2018 − 1 + t . 1 2018 2018 + t 2 − 2017 2018 .2 t ≥ 0 ∀ t ∈ − 1 ; 1 Suy ra
