Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số 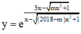 có 2 tiệm cận ngang?
có 2 tiệm cận ngang?
A. 2016
B. 2019
C. 2017
D. 2018
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

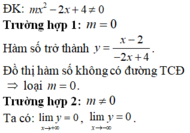
Suy ra đồ thị hàm số có 1 đường TCN y = 0.
Do đó đồ thị hàm số có đúng 2 đường tiệm cận đồ thị hàm số có đứng 1 đường tiệm cận đứng phương trình m x 2 - 2 x + 4 = 0 có nghiệm kép hoặc có 2 nghiệm phân biệt trong đó có 1 nghiệm x = 2.
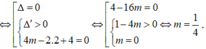
Vậy có 1 giá trị của m thỏa mãn yêu cầu bài toán.
Chọn A

Đáp án A
Đường thẳng y = y 0 được gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số y = f x nếu lim x → + ∞ f x = y 0 hoặc lim x → − ∞ f x = y 0
y = m x − x 2 − 2 x + 2 = m 2 x 2 − x 2 + 2 x − 2 m x + x 2 − 2 x + 2 = m 2 − 1 x 2 + 2 x − 2 m x + x 2 − 2 x + 2
Để hàm phân thức có tiệm cận ngang thì bậc tử phải nhỏ hơn hoặc bằng bậc mẫu ⇔ m 2 − 1 = 0 ⇔ m = 1 m = − 1
Vậy có 2 giá trị của m thỏa mãn yêu cầu bài toán.

Điều kiện: mx2+ 1 > 0.
- Nếu m= 0 thì hàm số trở thành y= x+ 1 không có tiệm cận ngang.
- Nếu m< 0 thì hàm số xác định ⇔ - 1 - m < x < 1 - m
Do đó, lim x → ± ∞ y không tồn tại nên đồ thị hàm số không có tiệm cận ngang.
- Nếu m> 0 thì hàm số xác định với mọi x.
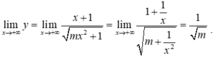
Suy ra đường thẳng y = 1 m là tiệm cận ngang của đồ thị hàm số khi x → + ∞ .

Suy ra đường thẳng y = - 1 m là tiệm cận ngang của đồ thị hàm số khi x → - ∞
Vậy m> 0 thỏa mãn yêu cầu đề bài.
Chọn D.
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số 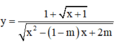 có hai tiệm cận đứng?
có hai tiệm cận đứng?
A. 3
B. 0
C. 2
D. 1

Đáp án C
Phương pháp: Để đồ thị hàm số có tiệm cận đứng x = x 0 thì x 0 là nghiệm của phương trình mẫu mà không là nghiệm của phương trình tử.
Cách giải:
ĐK: x ≥ - 1 và x 2 - ( 1 - m ) x + 2 m > 0
Xét phương trình 1 + x + 1 = 0 vô nghiệm
Xét phương trình x 2 - ( 1 - m ) x + 2 m = 0 (*). Để đồ thị hàmsố có hai TCĐ thì phương trình có 2 nghiệm phân biệt thỏa mãn ĐK x ≥ - 1
![]()

Khi đó gọi hai nghiệm của phương trình là x 1 > x 2 ta có:
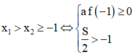
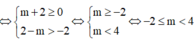
Kết hợp điều kiện ta có: 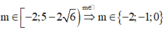
Thử lại:
Với ![]()
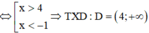
Khi đó hàm số có dạng 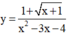 có 1 tiệm cận đứng x = 4 => Loại
có 1 tiệm cận đứng x = 4 => Loại
Với 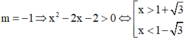
![]()
Khi đó hàm số có dạng  có 2 tiệm cận đứng x = 1±
3
=> TM
có 2 tiệm cận đứng x = 1±
3
=> TM
Khi 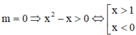
![]()
Khi đó hàm số có dạng 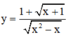 có 2 tiệm cận đứng x = 0; x = 1 => TM
có 2 tiệm cận đứng x = 0; x = 1 => TM
Vậy ![]()

Đáp án là B
Nhận xét:
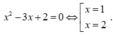
Đặt ![]()
Hàm số đã cho không có đường tiệm cận đứng khi và chỉ khi
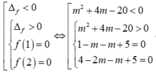
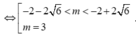
Vì m là số nguyên nên ![]()

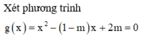
Đồ thị hàm số đã cho có 2 đường tiệm cận đứng ⇔ phương trình g(x) có 2 nghiệm phân biệt
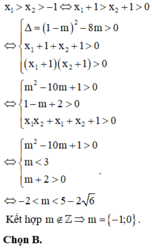
Đáp án B
Phương pháp:
Đồ thị của hàm số y = f(x) có hai tiệm cận ngang ó Tập xác định của y = f(x) chứa khoảng âm vô cực và dương vô cực và ∃ a,b ∈ R, a ≠ b: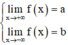
Cách giải: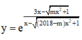
Điều kiện xác định: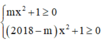
Đồ thị hàm số có 2 tiệm cận ngang => Tập xác định D phải chứa khoảng âm vô cực và dương vô cực
có 2 tiệm cận ngang => Tập xác định D phải chứa khoảng âm vô cực và dương vô cực
Ta tìm m để tồn tại giá trị của a ∈ R
TH1: . Khi đó
. Khi đó  R
R
TH2: . Khi đó
. Khi đó 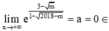 R
R
+) Giải phương trình:
Vậy, với mọi số nguyên hàm số
hàm số  luôn có 2 tiệm cận ngang.
luôn có 2 tiệm cận ngang.
Số giá trị nguyên của m thỏa mãn là: 2019 số.