Cho tam giác ABC và đường trung tuyến AM. Chứng minh SAMB = SAMC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
1 tháng 5 2019
Kẻ đường cao AH.
Ta có:
Mà BM = CM (vì AM là trung tuyến)
⇒ SAMB = SAMC (đpcm).
25 tháng 11 2022
a: Kẻ đường cao AH
\(S_{AMB}=\dfrac{1}{2}\cdot AH\cdot MB\)
\(S_{AMC}=\dfrac{1}{2}\cdot AH\cdot MC\)
mà MB=MC
nên \(S_{AMB}=S_{AMC}\)
MB=1/2BC
=>\(S_{AMB}=\dfrac{1}{2}\cdot AH\cdot\dfrac{1}{2}\cdot BC=\dfrac{1}{2}\cdot S_{ABC}\)
=>ĐPCM
b: Xét ΔABC có BC^2=AB^2+AC^2
nên ΔABC vuông tại A
AN=AC/2=4cm
\(S_{ANB}=\dfrac{1}{2}\cdot4\cdot6=2\cdot6=12\left(cm^2\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot6\cdot8=24\left(cm^2\right)\)
=>\(S_{BNC}=12\left(cm^2\right)\)
=>\(S_{BMN}=\dfrac{1}{2}\cdot12=6\left(cm^2\right)\)
5 tháng 3 2021
CM được \(\Delta\)ABC cân tại A (theo Cho tam giác ABC có đường tròn tiếp xúc với hai cạnh AB, AC và với hai trung tuyến BM, CN( M thuộc AC, N thuộc AB). Chứn... - Hoc24)
\(\Rightarrow\) AB = AC (t/c) (1)
Mà: M là trung điểm của AC; N là trung điểm của AB
\(\Rightarrow\) AM = AN (2)
Ta có: SAMB = SANC
\(\Rightarrow\) AM.MB = AN.NC
\(\Rightarrow\) \(\dfrac{AM}{AN}=\dfrac{NC}{MB}\)
Mà: AM = AN
\(\Rightarrow\) \(\dfrac{NC}{MB}=\dfrac{AM}{AM}=1\)
\(\Rightarrow\) NC = MB (3)
Cộng 2 vế của (1); (2); (3) ta được:
AM + MB + AB = AN + NC + AC (đpcm)
Chúc bn học tốt!
QT
1
DT
16 tháng 12 2021
vẽ đường cao AH chung của tam giác AMB và AMC
SAMB=\(\dfrac{1}{2}\)BM.AH
SAMC=\(\dfrac{1}{2}\)CM.AH
Vì AM là đường trung tuyến nên BM=MC
Do đó:SAMC=SAMB
( cái đường cao AH vuông góc với BC ă)
S
4 tháng 3 2023
câu 2 :
a) có phải là chứng minh AM ⊥ BC không
xét ΔAMB và ΔAMC, ta có :
AB = AC (2 cạnh bên của ΔABC cân tại A)
MB = MC (AM là đường trung tuyến của cạnh BC)
AM là cạnh chung
=> ΔAMB = ΔAMC (c.c.c)
=> \(\widehat{AMB}=\widehat{AMC}\) (2 cạnh tương ứng)
mà \(\widehat{AMB}+\widehat{AMC}=180^O\) (kề bù)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}=\dfrac{180^O}{2}=90^O\)
=> AM ⊥ BC
10 tháng 3 2023
Đề có sai không bạn , nếu `Delta ABC` là tam giác thường thôi thì không cm đc đâu ạ
N
21 tháng 8 2019
Lam truoc cau a nhe,toi roi
a.Vi tu giac AFME co 3 goc vuong va 2 duong cheo vuong goc voi nhau nen AFDE la hinh vuong.
Goi giao diem giua 2 duong cheo AM va EF do la Q
Suy ra:AQ=FQ nen tam giac AQF la tam giac vuong can hay \(\widehat{AQF}=45^0\left(1\right)\)
Tu giac QFKM co 3 goc vuong va MQ=FQ nen QFKM la hinh vuong.
Suy ra:FK=MK
Ta co:\(FK^2=MK.KC\Rightarrow FK=KC\)
Nen tam giac FKC la tam giac vuong can hay \(\widehat{C}=45^0\left(2\right)\)
Tu (1) va (2) suy ra:AM=MC
Hay AM la duong trung tuyen cua tam giac ABC.
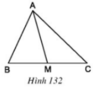
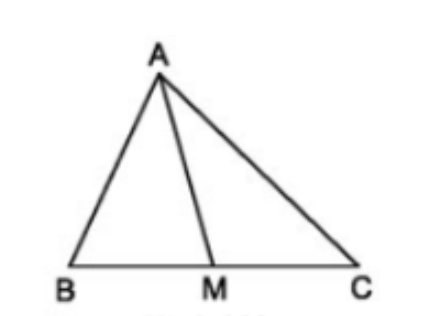
Kẻ đường cao AH
Ta có: SAMB = 0.5.BM.AH
SAMC = 0.5.CM.AH
Mà BM = CM (gt)
Þ SAMB = SAMC (ĐPCM)