Chứng minh phương trình sau luôn luôn có nghiệm: f ( x ) = ( m 2 - 2 m + 2 ) x 3 + 3 x - 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b, \(\Delta=\left(m+1\right)^2+8\left(m+3\right)=m^2+2m+1+8m+24\)
\(=m^2+10m+25=\left(m+5\right)^2\ge0\forall m\)
Vậy pt luôn có 2 nghiệm
a) Thay x = 2 vào phương trình ta có
\(2^2-\left(m+1\right)2-2\left(m+3\right)=0\Leftrightarrow m=2\)
Vậy để phương trình có nghiệm là x = 2 thì m = 2

\(f\left(x\right)=\left(1-m^2\right)\left(x+1\right)^3+x^2-x-3\) là hàm đa thức liên tục trên R. Do đó nó liên tục trên \(\left[-2;-1\right]\)
Ta có \(f\left(-1\right)=-1< 0\) và \(f\left(-2\right)=m^2+2>0\) nên \(f\left(-1\right)f\left(-2\right)< 0\) với mọi m.
Do đó, phương trình \(f\left(x\right)=0\) luôn có ít nhất một nghiệm trong khoảng (-2; -1) với mọi m. Nghĩa là, phương trình \(\left(1-m^2\right)\left(x+1\right)^3+x^2-x-3=0\) luôn có nghiệm với mọi m.

Xét pt cho là pt bậc hai một ẩn $x$ ( Với $a=1 \neq 0, b=-2(m-1), c = m-3$ )
Ta có : \(\Delta'=b'^2-ac\)
\(=\left[-\left(m-1\right)\right]^2-\left(m-3\right)\cdot1\)
\(=m^2-2m+1-m+3\)
\(=m^2-3m+4=\left(m-\dfrac{3}{2}\right)^2+\dfrac{7}{4}>0\)
Nên pt cho luôn có hai nghiệm phân biệt \(\forall m\)

\(\Delta'=\left(m-1\right)^2-\left(m+1\right)\left(m-3\right)=4>0\) ;\(\forall m\ne-1\)
\(\Rightarrow\) Pt luôn có 2 nghiệm pb với mọi \(m\ne-1\)

Đề bài không đúng, ví dụ với \(m=-1\) phương trình trở thành \(x^2-2x+5=0\) đây là một phương trình vô nghiệm


x2 - (2m + 3)x + 4m + 2 = 0
Có: \(\Delta\) = [-(2m + 3)]2 - 4.1.(4m + 2) = 4m2 + 12m + 9 - 16m - 8 = 4m2 - 4m + 1 = (2m - 1)2
Vì (2m - 1)2 \(\ge\) 0 với mọi m hay \(\Delta\) \(\ge\) 0
\(\Rightarrow\) Pt luôn có nghiệm với mọi m
Chúc bn học tốt!
Ta có: \(\Delta=\left(2m+3\right)^2-4\cdot1\cdot\left(4m+2\right)\)
\(\Leftrightarrow\Delta=4m^2+12m+9-4\left(4m+2\right)\)
\(\Leftrightarrow\Delta=4m^2+12m+9-16m-8\)
\(\Leftrightarrow\Delta=4m^2-4m+1\)
\(\Leftrightarrow\Delta=\left(2m-1\right)^2\ge0\forall m\)
Vậy: Phương trình luôn có nghiệm với mọi m

1) Ta có: \(\Delta=\left[-2\left(m-1\right)\right]^2-4\left(m-5\right)\)
\(=\left(2m-2\right)^2-4\left(m-5\right)\)
\(=4m^2-8m+4-4m+20\)
\(=4m^2-12m+24\)
\(=4m^2-12m+9+15\)
\(=\left(2m-3\right)^2+15>0\forall m\)
Do đó, phương trình luôn có hai nghiệm phân biệt với mọi m
2) Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)=2m-2\\x_1\cdot x_2=m-5\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}x_1+x_2=2m-2\\x_1-x_2=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x_1=2m+1\\x_1-x_2=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{2m+1}{2}\\x_2=x_1-3=\dfrac{2m+1}{2}-\dfrac{6}{2}=\dfrac{2m-5}{2}\end{matrix}\right.\)
Ta có: \(x_1\cdot x_5=m-5\)
\(\Leftrightarrow\left(2m+1\right)\left(2m-5\right)=4\left(m-5\right)\)
\(\Leftrightarrow4m^2-10m+2m-5=4m-20\)
\(\Leftrightarrow4m^2-8m-5-4m+20=0\)
\(\Leftrightarrow4m^2-12m+15=0\)(vô lý)
Vậy: Không có giá trị nào của m để phương tình có hai nghiệm mà hiệu của chúng bằng 3
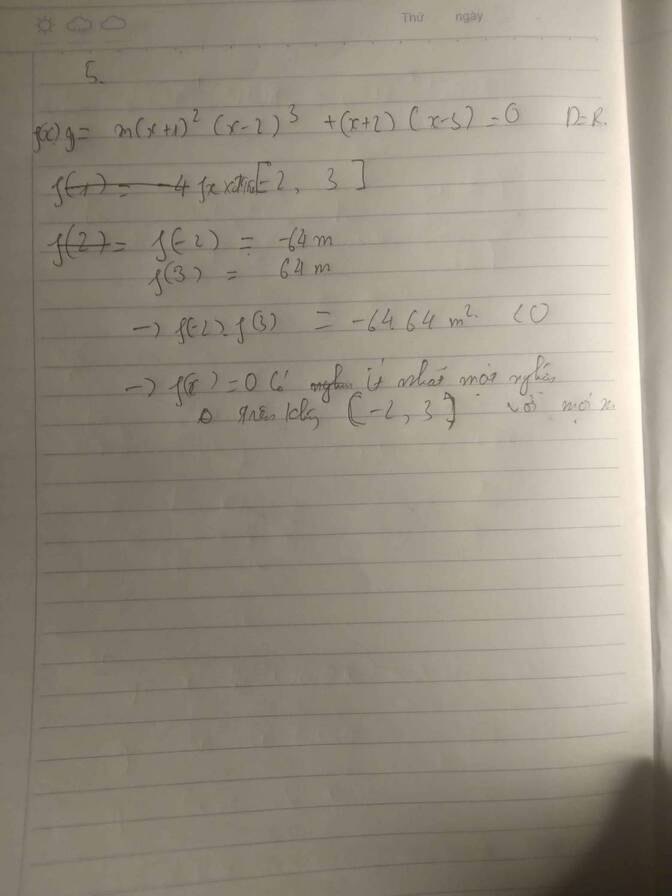
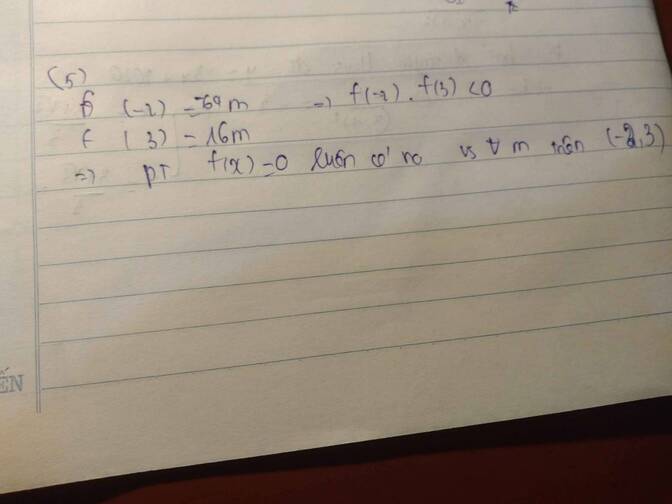
Xét hàm số f ( x ) = ( m 2 - 2 m + 2 ) x 3 + 3 x - 3 . Đây là hàm đa thức nên f(x) liên tục trên R.
- Suy ra: phương trình f(x) = 0 có ít nhất một nghiệm c ∈ (0;1)