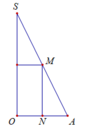
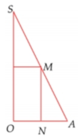
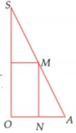
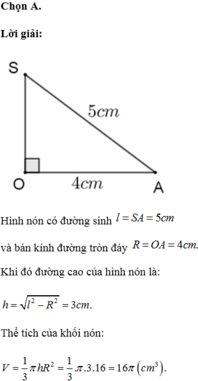
Cho tam giác SOA vuông tại O có MN//SO với M, N lần lượt nằm trên cạnh SA, OA như hình vẽ bên. Đặt SO = h không đổi. Khi quay hình vẽ quanh SO thì tạo thành một hình trụ nội tiếp hình nón đỉnh S có đáy là hình tròn tâm O bán kính R = OA. Tìm độ dài của MN theo h để thể tích khối trụ là lớn nhất
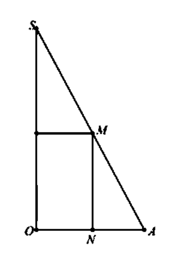
A. M N = h 2
B. M N = h 3
C. M N = h 4
D. M N = h 6

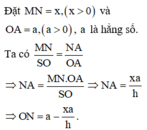
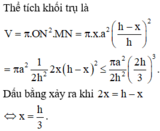

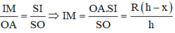
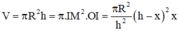
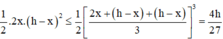
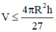 .
. 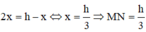



Đáp án B
Đặt SO' = x. Theo định lí Talet ta có: x h = r ' r 0 < x < h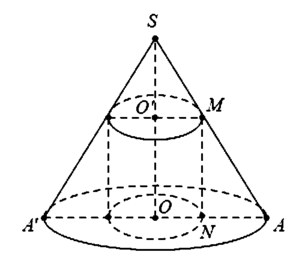
Thể tích khối trụ là V = πr ' 2 h - x = π xr 2 h 2 h - x = f x
Ta có f x = πr 2 h 2 x 2 h - x
Cách 1. Xét M x = x 2 h - x
Cách 2. Ta có M x = 4 . x 2 . x 2 . h - x ≤ 4 x 2 + x 2 + h - x 3 3 = 4 h 3 27
Dấu “=” xảy ra ⇔ x 2 = h - x ⇔ x = 2 3 h ⇒ M N = h - x = h 3 .