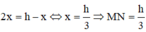Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

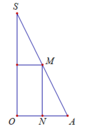
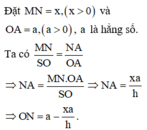
Khối trụ thu được có bán kính đáy bằng ON và chiều cao bằng MN.
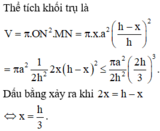
Chọn A

Đáp án B
Đặt SO' = x. Theo định lí Talet ta có:
x
h
=
r
'
r
0
<
x
<
h
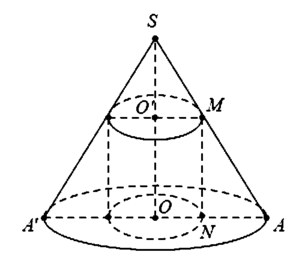
Thể tích khối trụ là V = πr ' 2 h - x = π xr 2 h 2 h - x = f x
Ta có f x = πr 2 h 2 x 2 h - x
Cách 1. Xét M x = x 2 h - x
Cách 2. Ta có M x = 4 . x 2 . x 2 . h - x ≤ 4 x 2 + x 2 + h - x 3 3 = 4 h 3 27
Dấu “=” xảy ra ⇔ x 2 = h - x ⇔ x = 2 3 h ⇒ M N = h - x = h 3 .

a: Xét tứ giác OBDC có
\(\widehat{OBD}+\widehat{OCD}=180^0\)
Do đó: OBDC là tứ giác nội tiếp
b: Xét ΔEBA và ΔECB có
\(\widehat{E}\) chung
\(\widehat{EAB}=\widehat{EBC}\)
Do đó: ΔEBA\(\sim\)ΔECB
Suy ra: EB/EC=EA/EB
hay \(EB^2=EC\cdot EA\)

hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m

a.có 18 HLP nhỏ có mặt được sơn xanh,1 HLP nhỏ có 1 mặt sơn xanh
b.có 24 HLP nhỏ được sơn đỏ ,có 12 HLP nhỏ đc sơn đỏ 2 mặt,12 HLP nhỏ đc sơn đỏ 1 mặt
c. có 3 HLP nhỏ không đc sơn mặt nào
tích mình nhé :D thanks
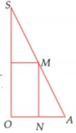
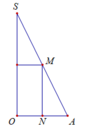
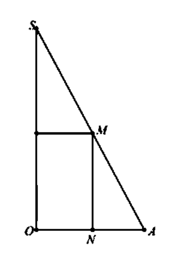

Đáp án B.
Khi quay hình vẽ quanh trục SO sẽ tạo nên khối trụ nội tiếp hình nón.
Suy ra thiết diện qua trục của hình trụ là hình chữ nhật MNPQ.
Theo định lí Talet, ta có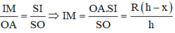
Thể tích khối trụ là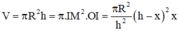
Theo AM – GM ta được
Vậy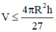 . Dấu “=” xảy ra khi
. Dấu “=” xảy ra khi