Tính giá trị của biểu thức
a)
b)
c)
d)
e)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

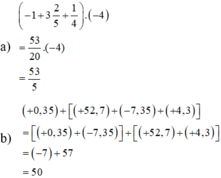
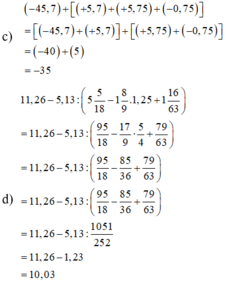
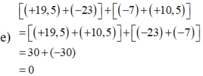

\(a,\) Số số hạng là \(\left(40-2\right):2+1=20\left(số\right)\)
Tổng là \(\left(40+2\right)\times20:2=420\)
\(b,\) Số số hạng là \(\left(39-1\right):2+1=20\left(số\right)\)
Tổng là \(\left(39+1\right)\times20:2=400\)
a) 2 + 4 + 6 + 8 + ... + 34 + 36 + 38 + 40
= ( 2 + 42 ) + ( 4 + 38 ) + .... + ( 20 + 22 )
= 42 \(\times\) 10
= 420
b) 1 + 3 + 5 + 7 + ... + 35 + 37 + 39
= ( 1 + 39 ) + ( 3 + 37 ) + ...+ ( 19 + 21 )
= 40 \(\times\) 10
= 400

2:
a: \(=\dfrac{1}{3}\left(-\dfrac{4}{5}-\dfrac{6}{5}\right)=-\dfrac{1}{3}\cdot2=-\dfrac{2}{3}\)
1:
\(A=7-\dfrac{3}{4}+\dfrac{1}{3}-6-\dfrac{5}{4}+\dfrac{4}{3}-5+\dfrac{7}{4}-\dfrac{5}{3}\)
\(=-4-\dfrac{1}{4}=-\dfrac{17}{4}\)
Bài 1:
\(A=\left(7-\dfrac{3}{4}+\dfrac{1}{3}\right)-\left(6+\dfrac{5}{4}-\dfrac{4}{3}\right)-\left(5-\dfrac{7}{4}+\dfrac{5}{3}\right)\)
\(A=7-\dfrac{3}{4}+\dfrac{1}{3}-6-\dfrac{5}{4}+\dfrac{4}{3}-5+\dfrac{7}{4}-\dfrac{5}{3}\)
\(A=\left(7-6-5\right)-\left(\dfrac{3}{4}+\dfrac{5}{4}-\dfrac{7}{4}\right)+\left(\dfrac{1}{3}+\dfrac{4}{3}-\dfrac{5}{3}\right)\)
\(A=-4-\dfrac{3+5-7}{4}+\dfrac{1+4-5}{3}\)
\(A=-4-\dfrac{1}{4}+\dfrac{0}{3}\)
\(A=-\dfrac{16}{4}-\dfrac{1}{4}+0\)
\(A=\dfrac{-16-1}{4}\)
\(A=-\dfrac{17}{4}\)
Bài 2:
\(\dfrac{1}{3}\cdot-\dfrac{4}{5}+\dfrac{1}{3}\cdot-\dfrac{6}{5}\)
\(=\dfrac{1}{3}\cdot\left(-\dfrac{4}{5}-\dfrac{6}{5}\right)\)
\(=\dfrac{1}{3}\cdot\dfrac{-4-6}{5}\)
\(=\dfrac{1}{3}\cdot\dfrac{-10}{5}\)
\(=\dfrac{1}{3}\cdot-2\)
\(=-\dfrac{2}{3}\)

a. 1/3 + 1/4 - 1/6
= 7/12 - 1/6
= 5/12
b. 2/5 x 5/7 : 3/4
= 2/7 : 3/4
= 8/21

a) \(\dfrac{1}{3}+\dfrac{4}{3}\times\dfrac{1}{2}=\dfrac{1}{3}+\dfrac{4}{6}=\dfrac{1}{3}+\dfrac{2}{3}=\dfrac{3}{3}=1\)
b) \(\dfrac{3}{5}\times\dfrac{4}{7}:\dfrac{16}{21}=\dfrac{3}{5}\times\dfrac{4}{7}\times\dfrac{21}{16}=\dfrac{12}{35}\times\dfrac{21}{16}=\dfrac{252}{560}=\dfrac{9}{20}\)

\(a,\Leftrightarrow\left[{}\begin{matrix}3x+2=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{2}{3}\left(l\right)\\x=-2\left(l\right)\end{matrix}\right.\Leftrightarrow x\in\varnothing\Leftrightarrow A\in\varnothing\\ b,\text{ý bạn là rút gọn A hả?}\\ A=\dfrac{x-2+2x+3x+6}{\left(x-2\right)\left(x+2\right)}=\dfrac{6x+4}{\left(x-2\right)\left(x+2\right)}\)

\(1,\\ a,2< 3\Rightarrow2^{30}< 3^{30}\Rightarrow-2^{30}>-3^{30}\\ b,6^{10}=6^{2\cdot5}=\left(6^2\right)^5=36^5>35^5\left(36>35\right)\)
\(2,\\ a,\dfrac{\left(-3\right)^{10}\cdot15^5}{25^3\cdot\left(-9\right)^7}=\dfrac{3^{10}\cdot5^5\cdot3^5}{5^6\cdot3^{14}}=\dfrac{3}{5}\\ b,\left(8x-1\right)^{2x+1}=5^{2x+1}\\ \Leftrightarrow8x-1=5\\ \Leftrightarrow x=\dfrac{3}{4}\)
Bài 2:
a: Ta có: \(\dfrac{\left(-3\right)^{10}\cdot15^5}{25^3\cdot\left(-9\right)^7}\)
\(=\dfrac{-3^{10}\cdot3^5\cdot5^5}{5^6\cdot3^{14}}\)
\(=-\dfrac{3}{5}\)
b: Ta có: \(\left(8x-1\right)^{2x+1}=5^{2x+1}\)
\(\Leftrightarrow8x-1=5\)
\(\Leftrightarrow8x=6\)
hay \(x=\dfrac{3}{4}\)

`a)100x^2-20x+1`
`=(10x-1)^2`
Thay `x=1/10`
`=>100x^2-20x+1=(1-1)^2=0`
`b)49x^2-42x+10`
`=49*4/49-42*2/7+10`
`=4-12+10=2`
`c)25x^2+40x+16y^2`
`=(5x+4y)^2=(2+3)^2=25`
Tính giá trị biểu thức
A= \(\left(4x^5+4x^4-5x^3+2x-2\right)^2+2020\) khi \(x=\dfrac{\sqrt{5}-1}{2}\)

Lời giải:
$x=\frac{\sqrt{5}-1}{2}$
$2x=\sqrt{5}-1$
$2x+1=\sqrt{5}\Rightarrow (2x+1)^2=5$
$\Leftrightarrow 4x^2+4x-4=0$
$\Leftrightarrow x^2+x-1=0$
Khi đó:
\((4x^5+4x^4-5x^3+2x-2)^2\)
\(=[4x^3(x^2+x-1)-x^3+2x-2]^2\)
\(=(-x^3+2x-2)^2=[-x(x^2+x+1)+(x^2+x-1)-1]^2\)
\(=(-1)^2=1\)

\(\sqrt{2-\sqrt{3}}\left(\sqrt{6}+\sqrt{2}\right)=\sqrt{4-2\sqrt{3}}\left(\sqrt{3}+1\right)=\sqrt{\left(\sqrt{3}-1\right)^2}\left(\sqrt{3}+1\right)\)
\(=\left|\sqrt{3}-1\right|\left(\sqrt{3}+1\right)=\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)=3-1=2\)
\(\dfrac{x-25}{\sqrt{x}-5}-\dfrac{x+4\sqrt{x}+4}{\sqrt{x}+2}=\dfrac{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}{\sqrt{x}-5}-\dfrac{\left(\sqrt{x}+2\right)^2}{\sqrt{x}+2}\)
\(=\sqrt{x}+5-\left(\sqrt{x}+2\right)=5-2=3\)
a: Ta có: \(\sqrt{2-\sqrt{3}}\cdot\left(\sqrt{6}+\sqrt{2}\right)\)
\(=\sqrt{4-2\sqrt{3}}\cdot\left(\sqrt{3}+1\right)\)
\(=\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)\)
=3-1
=2
b: Ta có: \(\dfrac{x-25}{\sqrt{x}-5}-\dfrac{x+4\sqrt{x}+4}{\sqrt{x}+2}\)
\(=\sqrt{x}+5-\sqrt{x}-2\)
=3

Bài 1:
\(A=\dfrac{-1}{3}+1+\dfrac{1}{3}=1\)
\(B=\dfrac{2}{15}+\dfrac{5}{9}-\dfrac{6}{9}=\dfrac{2}{15}-\dfrac{1}{9}=\dfrac{18-15}{135}=\dfrac{3}{135}=\dfrac{1}{45}\)
\(C=\dfrac{-1}{5}+\dfrac{1}{4}-\dfrac{3}{4}=\dfrac{-1}{5}-\dfrac{1}{2}=\dfrac{-7}{10}\)
Bài 2:
a: \(=\dfrac{1}{5}+\dfrac{1}{2}+\dfrac{2}{5}-\dfrac{3}{5}+\dfrac{2}{21}-\dfrac{10}{21}+\dfrac{3}{20}\)
\(=\left(\dfrac{1}{5}+\dfrac{2}{5}-\dfrac{3}{5}\right)+\left(\dfrac{2}{21}-\dfrac{10}{21}\right)+\left(\dfrac{1}{2}+\dfrac{3}{20}\right)\)
\(=\dfrac{-8}{21}+\dfrac{13}{20}=\dfrac{113}{420}\)
b: \(B=\dfrac{21}{23}-\dfrac{21}{23}+\dfrac{125}{93}-\dfrac{125}{143}=\dfrac{6250}{13299}\)
Bài 3:
\(\dfrac{7}{3}-\dfrac{1}{2}-\left(-\dfrac{3}{70}\right)=\dfrac{7}{3}-\dfrac{1}{2}+\dfrac{3}{70}=\dfrac{490}{210}-\dfrac{105}{210}+\dfrac{9}{210}=\dfrac{394}{210}=\dfrac{197}{105}\)
\(\dfrac{5}{12}-\dfrac{3}{-16}+\dfrac{3}{4}=\dfrac{5}{12}+\dfrac{3}{16}+\dfrac{3}{4}=\dfrac{20}{48}+\dfrac{9}{48}+\dfrac{36}{48}=\dfrac{65}{48}\)
Bài 4:
\(\dfrac{3}{4}-x=1\)
\(\Rightarrow-x=1-\dfrac{3}{4}\)
\(\Rightarrow x=-\dfrac{1}{4}\)
Vậy: \(x=-\dfrac{1}{4}\)
\(x+4=\dfrac{1}{5}\)
\(\Rightarrow x=\dfrac{1}{5}-4\)
\(\Rightarrow x=-\dfrac{19}{5}\)
Vậy: \(x=-\dfrac{19}{5}\)
\(x-\dfrac{1}{5}=2\)
\(\Rightarrow x=2+\dfrac{1}{5}\)
\(\Rightarrow x=\dfrac{11}{5}\)
Vậy: \(x=\dfrac{11}{5}\)
\(x+\dfrac{5}{3}=\dfrac{1}{81}\)
\(\Rightarrow x=\dfrac{1}{81}-\dfrac{5}{3}\)
\(\Rightarrow x=-\dfrac{134}{81}\)
Vậy: \(x=-\dfrac{134}{81}\)