Giải bất phương trình:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chị ơi phần a giải 2 theo 2TH. TH1 là 3 đều lớn hơn 0 và TH2 là 2 âm 1 dương
Phần b giải 3 TH: TH1 cả 3 nhỏ hơn 0
TH2 :2 dương 1 âm
TH3 : 1 âm 2 dương

a.
\(3\sqrt{-x^2+x+6}\ge2\left(1-2x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}-x^2+x+6\ge0\\1-2x< 0\end{matrix}\right.\\\left\{{}\begin{matrix}1-2x\ge0\\9\left(-x^2+x+6\right)\ge4\left(1-2x\right)^2\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}-2\le x\le3\\x>\dfrac{1}{2}\end{matrix}\right.\\\left\{{}\begin{matrix}x\le\dfrac{1}{2}\\25\left(x^2-x-2\right)\le0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}< x\le3\\\left\{{}\begin{matrix}x\le\dfrac{1}{2}\\-1\le x\le2\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow-1\le x\le3\)
b.
ĐKXĐ: \(x\ge0\)
\(\Leftrightarrow\sqrt{2x^2+8x+5}-4\sqrt{x}+\sqrt{2x^2-4x+5}-2\sqrt{x}=0\)
\(\Leftrightarrow\dfrac{2x^2+8x+5-16x}{\sqrt{2x^2+8x+5}+4\sqrt{x}}+\dfrac{2x^2-4x+5-4x}{\sqrt{2x^2-4x+5}+2\sqrt{x}}=0\)
\(\Leftrightarrow\dfrac{2x^2-8x+5}{\sqrt{2x^2+8x+5}+4\sqrt{x}}+\dfrac{2x^2-8x+5}{\sqrt{2x^2-4x+5}+2\sqrt{x}}=0\)
\(\Leftrightarrow\left(2x^2-8x+5\right)\left(\dfrac{1}{\sqrt{2x^2+8x+5}+4\sqrt{x}}+\dfrac{1}{\sqrt{2x^2-4x+5}+2\sqrt{x}}\right)=0\)
\(\Leftrightarrow2x^2-8x+5=0\)
\(\Leftrightarrow x=\dfrac{4\pm\sqrt{6}}{2}\)

a) Xét tam thức \(f\left( x \right) = 7{x^2} - 19x - 6\) có \(\Delta = 529 > 0\), có hai nghiệm phân biệt \({x_1} = - \frac{2}{7},{x_2} = 3\) và có \(a = 7 > 0\)
Ta có bảng xét dấu như sau

Vậy nghiệm của bất phương trình là đoạn \(\left[ { - \frac{2}{7};3} \right]\)
b) \( - 6{x^2} + 11x > 10 \Leftrightarrow - 6{x^2} + 11x - 10 > 0\)
Xét tam thức \(f\left( x \right) = - 6{x^2} + 11x - 10\) có \(\Delta = - 119 < 0\)và có \(a = - 6 < 0\)
Ta có bảng xét dấu như sau

Vậy bất phương trình vô nghiệm
c) \(3{x^2} - 4x + 7 > {x^2} + 2x + 1 \Leftrightarrow 2{x^2} - 6x + 6 > 0\)
Xét tam thức \(f\left( x \right) = 2{x^2} - 6x + 6\) có \(\Delta = - 12 < 0\)và có \(a = 2 > 0\)
Ta có bảng xét dấu như sau
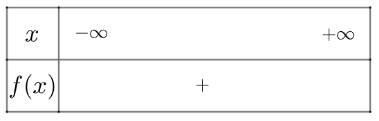
Vậy bất phương trình có vô số nghiệm
d) Xét tam thức \(f\left( x \right) = {x^2} - 10x + 25\) có \(\Delta = 0\), có nghiệm kép \({x_1} = {x_2} = 5\) và có \(a = 1 > 0\)
Ta có bảng xét dấu như sau

Vậy nghiệm của bất phương trình là \(x = 5\)

\(a,f'\left(x\right)=3x^2-6x\\ f'\left(x\right)\le0\Leftrightarrow3x^2-6x\le0\\ \Leftrightarrow3x\left(x-2\right)\le0\Leftrightarrow0\le x\le2\)
Lời giải:
a. $f'(x)\leq 0$
$\Leftrightarrow 3x^2-6x\leq 0$
$\Leftrightarrow x(x-2)\leq 0$
$\Leftrightarrow 0\leq x\leq 2$
b.
$f'(x)=x^2-3x+2=0$
$\Leftrightarrow 3x^2-6x=x^2-3x+2=0$
$\Leftrightarrow 3x(x-2)=(x-1)(x-2)=0$
$\Leftrightarrow x-2=0$
$\Leftrightarrow x=2$
c.
$g(x)=f(1-2x)+x^2-x+2022$
$g'(x)=(1-2x)'f(1-2x)'_{1-2x}+2x-1$
$=-2[3(1-2x)^2-6(1-2x)]+2x-1$
$=-24x^2+2x+5$
$g'(x)\geq 0$
$\Leftrightarrow -24x^2+2x+5\geq 0$
$\Leftrightarrow (5-12x)(2x-1)\geq 0$
$\Leftrightarrow \frac{-5}{12}\leq x\leq \frac{1}{2}$

a) Tam thức \(f(x) = - 5{x^2} + x - 1\) có \(\Delta = - 19 < 0\), hệ số \(a = - 5 < 0\) nên f(x) luôn âm (cùng dấu với a) với mọi x, tức là \(\)\( - 5{x^2} + x - 1 < 0\) với mọi \(x \in \mathbb{R}\). Suy ra bất phương trình có vô số nghiệm
b) Tam thức \(g(x) = {x^2} - 8x + 16\) có \(\Delta = 0\), hệ số a=1>0 nên g(x) luôn dương (cùng dấu với a) với mọi \(x \ne 4\), tức là \({x^2} - 8x + 16 > 0\) với mọi \(x \ne 4\)
Suy ra bất phương trình có nghiệm duy nhất là x = 4
c) Tam thức \(h(x) = {x^2} - x + 6\) có \(\Delta = - 23 < 0\), hệ số a=1>0 nên h(x) luôn dương (cùng dấu với a) với mọi x, tức là \({x^2} - x + 6 > 0\) với mọi \(x \in \mathbb{R}\). Suy ra bất phương trình có vô số nghiệm.


câu 1
a) 5x(x-2)=0 =>\(\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
b)(x+5)(2x-7)=0 =>\(\left[{}\begin{matrix}x+5=0\\2x-7=0\end{matrix}\right.\)=>\(\left[{}\begin{matrix}x=-5\\x=\dfrac{7}{2}\end{matrix}\right.\)
c) \(\dfrac{5x}{x+2}\)=4 Đk x\(\ne\)-2
=> 5x=4(x+2)
=>5x-4x=8
=>x=8(tmđk)
Chọn C
ĐKXĐ:
Bảng xét dấu
Dựa vào bảng xét dấu và đối chiếu điều kiện, ta có tập nghiệm của bất phương trình đã cho là