Trong hình thoi PQRS:
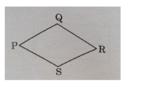
a) PQ là cạnh đối diện với ……….
b) PQ song song với ……….
c) PQ = ……….= ………. = ……….
d) PQ không song song với ………. và ……….
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) xet tam giac AQP va tam giac CQD ta co
AQ=QC ( Q la trung diem AC)
goc AQP=goc CQD ( 2 goc doi dinh)
goc PAQ=goc QCD ( 2 goc so le trong va AB//CD)
--> tam giac AQP=tam giac CQD (g-c-g)
--> PQ=QD ( 2 canh tuong ung )
--> Q la trung diem PD
b) TA CO
AP=DC ( tam giac AQP=tam giac CQD)
AP=PB ( P la trung diem AB)
--> DC=PB
xet tam giac BPC va tam giac PCD ta co
DC=PB (cmt)
PC=PC ( canh chung)
goc DCP=goc BPC ( 2 goc so le trong va AB//CD)
--> tam giac BPC=tam giac PCD ( c-g-c)
--> goc BCP=goc DPC (2 goc tuong ung)
ma goc BCP va goc DPC nam o vi tri so le trong
nen PQ//BC
ta co
PD= BC ( tam giac PDC= tam giac BPC)
PQ=1/2 PD ( Q la trung diem PD)
-->PQ=1/2 BC

a: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao và AM là phân giác của \(\widehat{BAC}\)
Xét tứ giác APMQ có
AP//MQ
AQ//MP
Do đó: APMQ là hình bình hành
Hình bình hành APMQ có AM là phân giác của góc PAQ
nên APMQ là hình thoi
b: Xét ΔABC có
M là trung điểm của BC
MP//AC
Do đó: P là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
MQ//AB
Do đó: Q là trung điểm của AC
Xét ΔABC có
P,Q lần lượt là trung điểm của AB,AC
=>PQ là đường trung bình của ΔABC
=>PQ//BC
c: Xét ΔABC có M,Q lần lượt là trung điểm của CB,CA
=>MQ là đường trung bình của ΔABC
=>MQ//AB và \(MQ=\dfrac{AB}{2}\)
mà \(MQ=\dfrac{MD}{2}\)
nên MD=AB
MQ//AB
=>MD//AB
Xét tứ giác ABMD có
AB//MD
AB=MD
Do đó: ABMD là hình bình hành
d: Xét tứ giác AMCD có
Q là trung điểm chung của AC và MD
Do đó: AMCD là hình bình hành
Hình bình hành AMCD có \(\widehat{AMC}=90^0\)
nên AMCD là hình chữ nhật
Hình chữ nhật AMCD muốn trở thành hình vuông thì CA là phân giác của góc MCD
=>\(\widehat{ACB}=\dfrac{1}{2}\cdot90^0=45^0\)
a) PQ là cạnh đối diện với SR
b) PQ song song với SR
c) PQ = QR = RS = SP
d) PQ không song song với QR và PS