Cho biết l i m x → 1 a x 2 + 1 - b x - 2 x 3 - 3 x + 2 ( a , b ∈ R ) có kết quả là một số thực. Giá trị của biểu thức a 2 + b 2 bằng
A. 45 16
B. 9 4
C. 97 - 48 3
D. 6 + 5 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

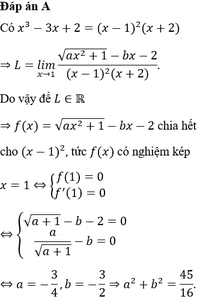

Bài 1:
\(P\left(-1\right)=-m-3=2\)
\(m=-3-2\)
\(m=-5\)
Bài 2:
Q(x) có nghiệm là -1⇔\(Q\left(-1\right)=0\)
⇒\(-2-m+7+3=0\)
\(m=7+3-2=8\)
Bài 3:
Q(x) có nghiệm là -1⇔\(Q\left(-1\right)=0\)
⇒\(m-2m-3=0\)
\(-m-3=0\)
\(m=-3\)

bài 2
A = 3+3^2 +3^3+ ...+3^100
3.A = 3^2+3^3+3^4+...+3^101
3.A-A=(3^2+3^3+3^4+...+3^101)-(3+3^2+3^3+...+3^100)
2.A=3^101-3
Ta có: 2A+3=3^ x
\(\Rightarrow\)(3^101-3)+3=3^x
\(\Rightarrow\)3^101-(3+3)=3^x
\(\Rightarrow\)3^101=3^x
\(\Rightarrow\)x=101
Vậy x=101

Bài 1 :
( 4x - 3 ) - ( x + 5 ) = 3 . ( 10 - x )
<=> 4x - 3 - x - 5 = 30 - 3x
=> 3x - 8 = 30 - 3x
=> 3x + 3x = 30 + 8
=> 6x = 38
=> x = \(\dfrac{19}{3}\)
Vậy x = \(\dfrac{19}{3}\)
Bài 2 :
Ta có : - f ( x ) = ( x - 1 ) . ( x + 2 ) = 0
=> x - 1 = 0 => x = 1
x + 2 = 0 => x = -2
- g ( 1 ) = 13 + a . 12 + b . 1 + 2 = 0
<=> 1 + a + b + 2 = 0
=> a = - 3 - b
- g ( -2 ) = ( -2 )3 + a . ( -2 )2 + b . ( -2 ) + 2 = 0
<=> - 8 + 4a - 2b + 2 = 0
hay -8 + 4 . ( -3 - b ) - 2b + 2 = 0
<=> -8 - 12 - 4b - 2b + 2 = 0
=> -18 - 6b = 0
=> b = -3
=> a = 0
Vậy a = 0 ; b= -3

Bài 1:
\(f\left(x\right)=5x-3.\)
+ \(f\left(x\right)=0\)
\(\Rightarrow5x-3=0\)
\(\Rightarrow5x=0+3\)
\(\Rightarrow5x=3\)
\(\Rightarrow x=3:5\)
\(\Rightarrow x=\frac{3}{5}\)
Vậy \(x=\frac{3}{5}.\)
+ \(f\left(x\right)=1\)
\(\Rightarrow5x-3=1\)
\(\Rightarrow5x=1+3\)
\(\Rightarrow5x=4\)
\(\Rightarrow x=4:5\)
\(\Rightarrow x=\frac{4}{5}\)
Vậy \(x=\frac{4}{5}.\)
+ \(f\left(x\right)=-2010\)
\(\Rightarrow5x-3=-2010\)
\(\Rightarrow5x=\left(-2010\right)+3\)
\(\Rightarrow5x=-2007\)
\(\Rightarrow x=\left(-2007\right):5\)
\(\Rightarrow x=-\frac{2007}{5}\)
Vậy \(x=-\frac{2007}{5}.\)
Làm tương tự với \(f\left(x\right)=2011.\)
Chúc bạn học tốt!

Bài 2:
\(M\left(3\right)=3^2-4\cdot3+3=0\)
=>x=3 là nghiệm của M(x)
\(M\left(-1\right)=\left(-1\right)^2-4\cdot\left(-1\right)+3=1+3+4=8\)
=>x=-1 không là nghiệm của M(x)

Bài 1.
a, (x-2)-15=65
x-2=65+15
x-2=80
x=80+2
x=2
b, 115-2\(\times\)(x-3)=35
2\(\times\)(x-3)=115-35
2\(\times\)(x-3)=70
x-3=70:2
x-3=35
x=35+5
x=38
c, 35+2\(\times\)(x-3)=65
2\(\times\)(x-3)=65-35
2\(\times\)(x-3)=30
x-3=30:2
x-3=15
x=15+3
x=18
3\(\times\)(x-5)-16=11
3\(\times\)(x-5)=11+16
3\(\times\)(x-5)=27
x-5=27:3
x-5=9
x=9+5
x=14
Bài 2:
a, \(2^x-1=31\)
\(2^x=31-1\)
\(2^x=30\)
\(\Rightarrow\)Không có x thoả mãn điều kiện \(2^x=30\)
b, \(x^3-1=26\)
\(x^3=26+1\)
\(x^3=27\)
\(\Rightarrow x=3\) vì \(3^3=27\)
c, \(6^x-1+1=37\)
\(6^x-1=37-1\)
\(6^x-1=36\)
\(6^x=36+1\)
\(6^x=37\)
\(\Rightarrow\) Không có x thoả mãn điều kiện \(6^x=37\)
d, (x+2)\(^3\)-15\(^0\)=215
\(\left(x+2\right)^3-1=215\)
\(\left(x+2\right)^3=215+1\)
\(\left(x+2\right)^3=216\)
\(\left(x+2\right)^3=6^3\)
\(x+2=6\)
\(x=6-2\)
\(x=4\)
e, \(2\times\left(x-9\right)^2=2\)
\(\left(x-9\right)^2=2:2\)
\(\left(x-9\right)^2=1\)
\(\Rightarrow x-9=1\) vì \(1^2=1\)
x=1+9
x=10
g, \(3\times\left(x-5\right)^3=51\)
\(\left(x-5\right)^3=51:3\)
\(\left(x-5\right)^3=17\)
\(\Rightarrow\) Không có x thoả mãn điều kiện \(\left(x-5\right)^3=17\)
Nếu đúng thì tick cho mk nhé ![]()
Bài 1:
a)\(\left(x-2\right)-15=65\)
\(x-2=65+15\)
\(x-2=80\)
\(x=80+2\)
\(x=82\)
b)\(115-2\left(x-3\right)=35\)
\(2\left(x-3\right)=115-35\)
\(2\left(x-3\right)=80\)
\(x-3=80:2\)
\(x-3=40\)
\(x=40+3\)
c) \(35+2\left(x-3\right)=65\)
\(2\left(x-3\right)=65-35=30\)
\(x-3=30:2=15\)
\(x=15+3=18\)
d) \(3\left(x-5\right)-16=11\)
\(3\left(x-5\right)=11+16=27\)
\(x-5=27:3=9\)
\(x=9+5=14\)
Bài 2:
a) \(2^x-1=31\)
\(2^x=31+1=32\)
Vì \(2^5=32\Rightarrow x=5\)
b) \(x^3-1=26\)
\(x^3=26+1=27\)
Vì \(3^3=27\Rightarrow x=3\)
c)\(6^{x-1}+1=37\)
\(6^{x-1}=37-1=36\)
Vì \(6^6=36\Rightarrow x-1=6\Rightarrow x=6+1=7\)
d)\(\left(x+2\right)^3-15^0=215\)
\(\left(x+2\right)^3-1=215\)
\(\left(x+2\right)^3=215+1=216\)
Vì \(6^3=216\Rightarrow x+2=6\Rightarrow x=6-2=4\)
e)\(2\left(x-9\right)^2=2\)
\(\left(x-9\right)^2=2:2=1\)
Vì \(1^2=1\Rightarrow x-9=1\Rightarrow x=1+9=10\)
g) \(3\left(x-5\right)^3=51\)
\(\left(x-5\right)^3=51:3=17\)

Bài 1:
Từ P(x) = 3x2+8x-4 = -4
=> 3x2+8x = 0
x(3x+8) = 0
=> x = 0 3x+8 = 0
=> x = 0 3x = 8
=> x = 8/3
Bài 2 :
Ta có x = -1 là nghiệm của đa thức f(x) = 2x2-x+m
=> f(-1) = 2(-1)2-(-1)+m = 0
=> 2+1+m = 0
=> 3+m = 0
m = 0-3
m = -3

Câu 1:
Ta có: \(M\left(x\right)=6x^3+2x^4-x^2+3x^2-2x^3-x^4+1-4x^3\)
\(=x^4+2x^2+1\)
\(=\left(x^2+1\right)^2\ge1\forall x\)
hay M(x) vô nghiệm(đpcm)
Câu 2:
Ta có: A(0)=5
\(\Leftrightarrow m+n\cdot0+p\cdot0\cdot\left(0-1\right)=5\)
\(\Leftrightarrow m=5\)
Ta có: A(1)=-2
\(\Leftrightarrow m+n\cdot1+p\cdot1\cdot\left(1-1\right)=-2\)
\(\Leftrightarrow5+n=-2\)
hay n=-2-5=-7
Ta có: A(2)=7
\(\Leftrightarrow5+\left(-7\right)\cdot2+p\cdot2\cdot\left(2-1\right)=7\)
\(\Leftrightarrow-9+2p=7\)
\(\Leftrightarrow2p=16\)
hay p=8
Vậy: Đa thức A(x) là 5-7x+8x(x-1)
\(=5-7x+8x^2-8x\)
\(=8x^2-15x+5\)

1.
a. \((x+1)(x^2-x+1)-(x-1)(x^2+x+1)\)
\(=x^3 + 1-(x^3-1) = 2 \)
b.
\(\dfrac{2x^2-4x+2}{2x-2}=\dfrac{2\left(x^2-2x+1\right)}{2\left(x-1\right)}=\dfrac{\left(x-1\right)^2}{x-1}=x-1\)
2.
a. \(x^2-4y^2+12y-9=x^2-\left[\left(2y\right)^2-2\cdot2y\cdot3+3^2\right]=x^2-\left(2y-3\right)^2=\left(x-2y+3\right)\left(x+2y-3\right)\)
b.
\(5x^2+3\left(x+y\right)^2-5y^2\)
\(=3\left(x+y\right)^2+5\left(x^2-y^2\right)\)
\(=3\left(x+y\right)^2+5\left(x+y\right)\left(x-y\right)\)
\(=\left(x+y\right)\left[3\left(x+y\right)+5\left(x-y\right)\right]\)
\(=\left(x+y\right)\left(3x+3y+5x-5y\right)\)
\(=\left(x+y\right)\left(8x-2y\right)=2\left(x+y\right)\left(4x-y\right)\)