Gọi A', B', C' tương ứng là ảnh của ba điểm A, B, C qua phép đồng dạng tỉ số k. Chứng minh rằng: A ' B ' → . A ' C ' → = k 2 . A B → . A C →
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Để ý rằng
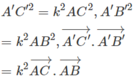
Ta có:
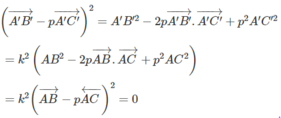
Từ đó suy ra 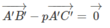
Giả sử ba điểm A, B, C thẳng hàng và điểm B nằm giữa hai điểm A và C. Khi đó A B → = t A C → , với 0 < t < 1. Áp dụng bài 1.39 ta cũng có A ' B → = t A ' C ' → , với 0 < t < 1. Do đó ba điểm A′, B′, C′ thẳng hàng và điểm B' nằm giữa hai điểm A' và C'.

A’, B’ lần lượt là ảnh của A, B qua phép đồng dạng F, tỉ số k ⇒ A’B’= kAB
M’ = F(M) ⇒ A’M’ = kAM
M là trung điểm AB ⇒ AM = 1/2 AB ⇒ kAM = 1/2 kAB hay A’M’= 1/2 A’B’
Vậy M’ là trung điểm của A’B’

Gọi AD và A'D' lần lượt là phân giác của tam giác ABC tại góc BAC và tam giác A'B'C' tại góc B'A'C'
tam giác ABC ~ tam giác A'B'C' => góc BAC = góc B'A'C'
=> góc BAD = 1/2 góc BAC = 1/2 góc B'A'C' = góc B'A'D' (AD và A'D' là phân giác)
Xét tam giác ABD và tam giác A'B'D' có :
1. góc ABD = góc A'B'D' ( do tam giác ABC ~ tam giác A'B'C' )
2. góc BAD = góc B'A'D' ( cmt )
Vậy tam giác ABD ~ tam giác A'B'D' (g-g)
=> AD/A'D' = AB/A'B' = k
CMTT cho phân giác 2 góc còn lại ta cũng có điều cần chứng minh.

