Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

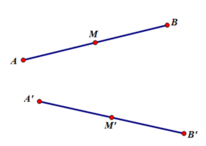
Gọi A', B', M' lần lượt là ảnh của A, B, M qua phép dời hình F
Theo tính chất 1 ⇒ AB = A'B' và AM = A'M' (1)
M là trung điểm AB ⇒ AM = 1/2 AB
Kết hợp (1) ⇒ A'M' = 1/2 A'B' ⇒ M' là trung điểm A'B'

a) Gọi H là trung điểm của BC
△ABC có: E là trung điểm của AC, H là trung điểm của BC
Suy ra: EH // AB
Mà AB // A'B'
Do đó: EH // A'B' hay EH // B'F (1)
Ta có: EH // AB nên \(\dfrac{EH}{AB}=\dfrac{EC}{AC}=\dfrac{1}{2}\)
Mà AB = A'B', B'F = \(\dfrac{1}{2}\) A'B'
Nên: EH = B'F (2)
(1)(2) suy ra: EHB'F là hình bình hành. Do đó: EF // B'H
Mà B'H thuộc (BCC'B')
Suy ra: EF // (BCC'B')
b) Gọi K là trung điểm AB
Dễ dàng chứng minh được FKBB' là hình bình hành
Ta có: FK // BB'
Mà BB' // CC'
Suy ra: FK // CC' (1)
Ta có: FK = BB', mà BB' = CC'
Do đó: FK = CC' (2)
(1)(2) suy ra FKCC' là hình bình hành
Mà hai đường chéo của hình bình hành cắt nhau tại trung điểm mỗi đường
Nên C'K cắt CF tại trung điểm của hai đường thẳng
mà C'K thuộc (AC'B) , CF cắt (AC'B) tại I (đề bài)
Do đó: I là trung điểm của CF.

Để ý rằng
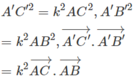
Ta có:
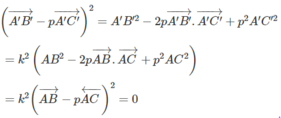
Từ đó suy ra 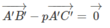
Giả sử ba điểm A, B, C thẳng hàng và điểm B nằm giữa hai điểm A và C. Khi đó A B → = t A C → , với 0 < t < 1. Áp dụng bài 1.39 ta cũng có A ' B → = t A ' C ' → , với 0 < t < 1. Do đó ba điểm A′, B′, C′ thẳng hàng và điểm B' nằm giữa hai điểm A' và C'.

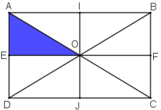
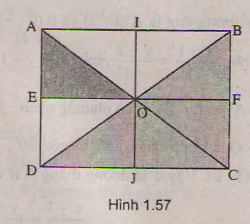
+ Lấy đối xứng qua đường thẳng IJ.
IJ là đường trung trực của AB và EF
⇒ ĐIJ(A) = B; ĐIJ (E) = F
O ∈ IJ ⇒ ĐIJ (O) = O
⇒ ĐIJ (ΔAEO) = ΔBFO
+ ΔBFO qua phép vị tự tâm B tỉ số 2
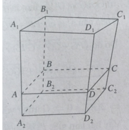
Vậy ảnh của ΔAEO qua phép đồng dạng theo đề bài là ΔBCD.


+ Ta đi xác định đường thẳng ∆:
Giả sử đã dựng được đường thẳng ∆ cắt cả AN và A’B. Gọi I; J lần lượt là giao điểm của ∆ với AN và A’B.
Xét phép chiếu song song lên (ABCD) theo phương chiếu A’B.
Khi đó ba điểm J; I; M lần lượt có hình chiếu là B; I’; M
Do J; I; M thẳng hàng nên B; I’; M cũng thẳng hàng. Gọi N’ là hình chiếu của N thì AN’ là hình chiếu của AN.
Vì I thuộc AN nên I’ thuộc AN’
=> I ‘ là giao điểm của BM và AN’.
Từ trên suy ra cách dựng:
+ Gọi I’ là giao điểm của AN’ và BM.
+Trong ( ANN’) dựng II’// NN’( đã có NN’// CD’) cắt AN tại I .
+Vẽ đường thẳng MI, đó chính là đường thẳng cần dựng.
+ Tính tỉ số:
Ta có MC= CN’ suy ra MN’= CD= AB. Do đó I’ là trung điểm của BM.
Mặt khác II’// JB nên II’ là đường trung bình của tam giác MBJ, suy ra IM= IJ nên I M I J = 1
Chọn B

Phép đối xứng qua đường thẳng ***** biến tam giác AEO thành tam giác BFO, phép vị tự tâm B, tỉ số 2 biến tam giác BFO thành tam giác BCD. Do đó ảnh của tam giác AEO qua phép đồng dạng đã cho là tam giác BCD.
Phép đối xứng qua đường thẳng biến tam giác AEO thành tam giác BFO, phép vị tự tâm B, tỉ số 2 biến tam giác BFO thành tam giác BCD. Do đó ảnh của tam giác AEO qua phép đồng dạng đã cho là tam giác BCD.



A’, B’ lần lượt là ảnh của A, B qua phép đồng dạng F, tỉ số k ⇒ A’B’= kAB
M’ = F(M) ⇒ A’M’ = kAM
M là trung điểm AB ⇒ AM = 1/2 AB ⇒ kAM = 1/2 kAB hay A’M’= 1/2 A’B’
Vậy M’ là trung điểm của A’B’