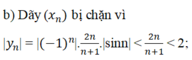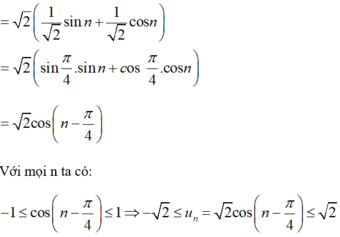Xét tính bị chặn của các dãy số với số hạng tổng quát sau:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

![]()

a) Ta có: \( - 1 \le \cos \frac{\pi }{n} \le 1,\forall n \in {\mathbb{N}^*} \Leftrightarrow - 1 \le {a_n} \le 1,\forall n \in {\mathbb{N}^*}\).
Vậy dãy số \(\left( {{a_n}} \right)\) bị chặn.
b) \(\forall n \in {\mathbb{N}^*}\) ta có:
\(n > 0 \Leftrightarrow n + 1 > 0 \Leftrightarrow \frac{n}{{n + 1}} > 0 \Leftrightarrow {b_n} > 0\). Vậy \(\left( {{b_n}} \right)\) bị chặn dưới.
\({b_n} = \frac{n}{{n + 1}} = \frac{{\left( {n + 1} \right) - 1}}{{n + 1}} = 1 - \frac{1}{{n + 1}}\)
Vì \(n + 1 > 0 \Leftrightarrow \frac{1}{{n + 1}} > 0 \Leftrightarrow - \frac{1}{{n + 1}} < 0 \Leftrightarrow 1 - \frac{1}{{n + 1}} < 1 \Leftrightarrow {b_n} < 1\). Vậy \(\left( {{b_n}} \right)\) bị chặn trên.
Ta thấy dãy số \(\left( {{b_n}} \right)\) bị chặn trên và bị chặn dưới nên dãy số \(\left( {{b_n}} \right)\) bị chặn.


a) Ta có: \({u_{n + 1}} = \frac{{{{\left( {n + 1} \right)}^2}}}{{n + 1 + 1}} = \frac{{{{\left( {n + 1} \right)}^2}}}{{n + 2}}\)
Xét hiệu \({u_{n + 1}} - {u_n} = \frac{{{{\left( {n + 1} \right)}^2}}}{{n + 2}} - \frac{{{n^2}}}{{n + 1}} = \frac{{{{\left( {n + 1} \right)}^3} - {n^2}\left( {n + 2} \right)}}{{\left( {n + 2} \right)\left( {n + 1} \right)}} = \frac{{{n^3} + 3{n^2} + 3n + 1 - {n^3} - 2{n^2}}}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\)
\( = \frac{{{n^2} + 3n + 1}}{{\left( {n + 2} \right)\left( {n + 1} \right)}} > 0\) với mọi n ∈ ℕ*.
Vì vậy dãy số đã cho là dãy số tăng.
b) Ta có: \({u_{n + 1}} = \frac{2}{{{5^{n + 1}}}}\)
Xét hiệu \({u_{n + 1}} - {u_n} = \frac{2}{{{5^{n + 1}}}} - \frac{2}{{{5^n}}} = - \frac{4}{5}.\frac{2}{{{5^n}}} = - \frac{8}{{{5^{n + 1}}}} < 0\)
Vì vậy dãy số đã cho là dãy số giảm.

a) \(\forall n \in {\mathbb{N}^*}\) ta có:
\(\left. \begin{array}{l}0 \le {\sin ^2}\frac{{n\pi }}{3} \le 1\\ - 1 \le \cos \frac{{n\pi }}{4} \le 1\end{array} \right\} \Leftrightarrow 0 + \left( { - 1} \right) \le {\sin ^2}\frac{{n\pi }}{3} + \cos \frac{{n\pi }}{4} \le 1 + 1 \Leftrightarrow - 1 \le {a_n} \le 2\).
Vậy dãy số \(\left( {{a_n}} \right)\) bị chặn.
b) Ta có: \({u_n} = \frac{{6n - 4}}{{n + 2}} = \frac{{6\left( {n + 2} \right) - 16}}{{n + 2}} = 6 - \frac{{16}}{{n + 2}}\)
\(\forall n \in {\mathbb{N}^*}\) ta có:
\(n + 2 > 0 \Leftrightarrow \frac{{16}}{{n + 2}} > 0 \Leftrightarrow 6 - \frac{{16}}{{n + 2}} < 6 \Leftrightarrow {u_n} < 6\). Vậy \(\left( {{u_n}} \right)\) bị chặn trên.
\(n \ge 1 \Leftrightarrow n + 2 \ge 1 + 2 \Leftrightarrow n + 2 \ge 3 \Leftrightarrow \frac{{16}}{{n + 2}} \le \frac{{16}}{3} \Leftrightarrow 6 - \frac{{16}}{{n + 2}} \ge 6 - \frac{{16}}{3} \Leftrightarrow {u_n} \ge \frac{2}{3}\)
Vậy \(\left( {{u_n}} \right)\) bị chặn dưới.
Ta thấy dãy số \(\left( {{u_n}} \right)\) bị chặn trên và bị chặn dưới nên dãy số \(\left( {{u_n}} \right)\) bị chặn.