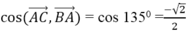Cho hình vuông ABCD. Tính cos A C → ; B A →
A. -1
B. - 2 2
C. 0
D. 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 7 2017
Theo định lý cosin ta có
\(AD^2=AM^2+MD^2-2.MA.MD.cos\widehat{ÀMD}\)
Xé \(\Delta ABM\)có \(BM=\frac{a}{2}\)
\(AM=\sqrt{AB^2+BM^2}=\sqrt{a^2+\left(\frac{a}{2}\right)^2}=\frac{\sqrt{5}a}{2}\)
Xét \(\Delta DCM\)có \(CM=\frac{a}{2}\)
\(\Rightarrow DM=\sqrt{DC^2+CM^2}=\sqrt{a^2+\left(\frac{a}{2}\right)^2}=\frac{\sqrt{5}a}{2}\)
\(\Rightarrow\cos\widehat{AMD}=\frac{AM^2+MD^2-AD^2}{2.MA.MD}=\frac{\frac{5a^2}{4}+\frac{5a^2}{4}-a^2}{\frac{\sqrt{5}a}{2}.\frac{\sqrt{5}a}{2}}=\frac{3}{5}\)
Vậy \(\cos\widehat{AMD}=\frac{3}{5}\)
CM
21 tháng 3 2019
Chọn A.
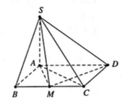
Gắn tọa độ Oxyz, với A(0;0;0), B(1;0;0), D(0;3;0), S(0;0;1)
Khi đó C ( 1 ; 3 ; 0 ) ⇒ Trung điểm M của BC là M ( 1 ; 3 2 ; 0 ) .
Ta có
SM → = ( 1 ; 3 2 ; - 1 ) , SD → = ( 0 ; 3 ; - 1 ) ⇒ [ SM → ; SD → ] = ( 3 2 ; 1 ; 3 ) .
Suy ra n ⃗ ( SDM ) = ( 3 2 ; 1 ; 3 ) mà n ⃗ ( ABCD ) = n ⃗ ( Oxy ) = ( 0 ; 0 ; 1 ) ,
ta được
cos ( SDM ^ ) ; ( ABCD ) = n → ( SDM ) . n → ( ABCD ) n → ( SDM ) . n → ( ABCD ) = 6 7 .
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 4 2023
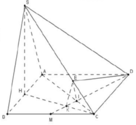
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\AD\perp CD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
Mà CD là giao tuyến (SCD) và (ABCD)
\(\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ABCD)
\(\Rightarrow\widehat{SDA}=60^0\Rightarrow SA=AD.tan60^0=3a\)
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
Mà \(BC=\left(SBC\right)\cap\left(ABCD\right)\Rightarrow\widehat{SBA}\) là góc giữa (SBC) và (ABCD)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=3\Rightarrow\widehat{SBA}=...\)
b.
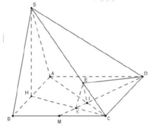
Từ A kẻ \(AE\perp BD\)
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\)
\(\Rightarrow BD\perp\left(SAE\right)\Rightarrow\widehat{SEA}\) là góc giữa (SBD) và (ABCD)
Hệ thức lượng: \(\dfrac{1}{AE^2}=\dfrac{1}{AB^2}+\dfrac{1}{AD^2}\Rightarrow AE=\dfrac{a\sqrt{3}}{2}\)
\(tan\widehat{SEA}=\dfrac{SA}{AE}=2\sqrt{3}\Rightarrow\widehat{SEA}=...\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 4 2023
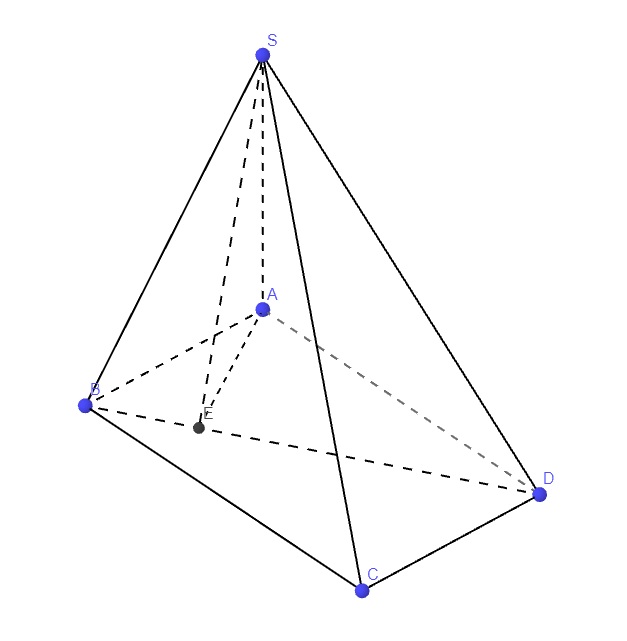
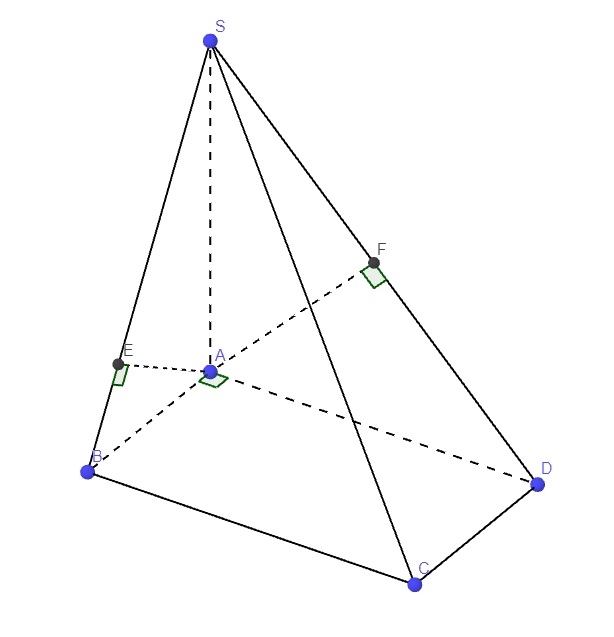
Lần lượt kẻ \(AE\perp SB\) (1) và \(AF\perp SD\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC\perp AE\) (2)
(1);(2) \(\Rightarrow AE\perp\left(SBC\right)\)
Hoàn toàn tương tự ta có \(AF\perp\left(SCD\right)\)
\(\Rightarrow\) Góc giữa (SBC) và (SCD) là góc giữa AE và AF
Cũng từ \(BC\perp\left(SAB\right)\) mà \(BC=\left(SBC\right)\cap\left(ABCD\right)\Rightarrow\widehat{SBA}\) là góc giữa (SBCD) và đáy
\(\Rightarrow\widehat{SBA}=60^0\Rightarrow SA=AB.tan60^0=a\sqrt{3}\)
Hệ thức lượng: \(\dfrac{1}{AE^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}\Rightarrow AE=\dfrac{a\sqrt{3}}{2}\)
\(\dfrac{1}{AF^2}=\dfrac{1}{SA^2}+\dfrac{1}{AD^2}\Rightarrow AF=\dfrac{a\sqrt{6}}{2}\)
\(SB=\sqrt{SA^2+AB^2}=2a\) ; \(SD=a\sqrt{6}\)
\(BD=\sqrt{AB^2+AD^2}=2a\Rightarrow cos\widehat{BSD}=\dfrac{SB^2+SD^2-BD^2}{2SB.SD}=\dfrac{\sqrt{6}}{4}\)
\(SE=\sqrt{SA^2-AE^2}=\dfrac{3a}{2}\) ; \(SF=\sqrt{SA^2-AF^2}=\dfrac{a\sqrt{6}}{2}\)
\(\Rightarrow EF=\sqrt{SE^2+SF^2-2SE.SF.cos\widehat{BSD}}=\dfrac{a\sqrt{6}}{2}\)
\(\Rightarrow cos\widehat{EAF}=\dfrac{AE^2+AF^2-EF^2}{2AE.AF}=\dfrac{\sqrt{2}}{4}\)
TP
0
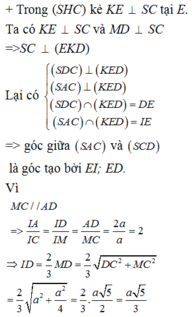
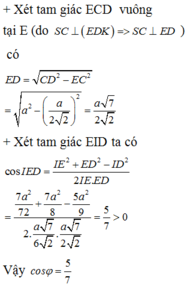
Chọn B.
Ta có:
Khi đó