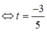Điểm M thuộc đường thẳng d : x = - 1 - t y = 2 t , t ∈ ℝ và cách điểm N(2;0) một khoảng ngắn nhất có tọa độ là:
A. ( - 3 5 ; - 4 5 )
B. ( - 2 5 ; - 6 5 )
C. ( - 1 ; 0 )
D. ( - 2 ; 2 )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do A nằm trên d nên thay tọa độ điểm A vào phương trình tham số đường thẳng d:
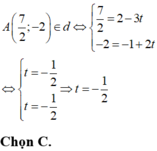

Thế 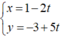 vào phương trình của d’ ta được:
vào phương trình của d’ ta được:
3( 1-2t) -2( -3+5t) -1 =0 hay -16t + 8= 0
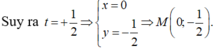
Chọn C.

a) Hai điểm A và B cùng thuộc dường thẳng a
b) Đường thẳng b không đi qua 2 điểm M và N
c) Đường thẳng c đi qua 2 điểm H, K và không chứa hai điểm U, V
d) Điểm X nằm trên cả 2 đường thẳng d và t, điểm Y chỉ thuộc đường thẳng d và nằm ngoài đường thẳng t, đường thẳng t đi qua điểm Z, còn đường thẳng d không chứa điểm Z
a) Hai điểm A và B cùng thuộc dường thẳng a
b) Đường thẳng b không đi qua 2 điểm M và N
c) Đường thẳng c đi qua 2 điểm H, K và không chứa hai điểm U, V
d) Điểm X nằm trên cả 2 đường thẳng d và t, điểm Y chỉ thuộc đường thẳng d và nằm ngoài đường thẳng t, đường thẳng t đi qua điểm Z, còn đường thẳng d không chứa điểm Z
e) Điểm U nằm trên cả hai đường thẳng m, n và không thuộc đường thẳng p; điểm V thuộc cả hai đường thẳng n, p và nằm ngoài đường thẳng m; hai đường thẳng p, m cùng đi qua điểm R còn đường thẳng n không chứa điểm R

Đáp án: A

Vì d vuông góc với d’ nên d sẽ nhận vecto chỉ phương của d’ làm vecto pháp tuyến
Vậy d là đường thẳng đi qua M và có vecto pháp tuyến là 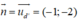
d: -1(x - 2) - 2(y + 3) = 0 ⇔ -x - 2y - 4 ⇔ x + 2y + 4 = 0

Chọn B

Vậy M(3;−4;−2) là giao điểm của đường thẳng d và mặt phẳng (P).

Lấy điểm M( 2+ 2t; 3+ t) nằm trên d;
![]()
Để AM= 5 khi và chỉ khi
(2t+2) 2+ (t+2) 2= 25 hay 5t2+12t- 17= 0
Suy ra t= 1 hoặc t= - 17/5
Với t= 1 thì M( 4;4)
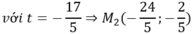
Chọn C.

Làm: (d) y\(=\) (m-1)x+m+3
b, Để (d) cắt đường y=-x+1 trên Oy thì
\(\left\{{}\begin{matrix}a\ne a'\\b=b'\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m-1\ne-1\\1=m+3\end{matrix}\right.\Leftrightarrow m=-2\)
Kl:............
a, Để (d) cắt đường y=x+2 thì a\(\ne a'\Leftrightarrow m-1\ne1\Leftrightarrow m\ne2\)
Khi m khác 2 ta giả sử (d) cắt đường y=x+2 tại điểm A(x';y') thì
\(\left\{{}\begin{matrix}y'=\left(m-1\right)x+m+3\\y'=x'+2\end{matrix}\right.\)
\(\Rightarrow\left(m-1\right)x+m+3=x'+2\)
\(\Leftrightarrow x'\left(m-2\right)=-1-m\)
\(\Leftrightarrow x'=\frac{-1-m}{m-2}\left(v\text{ì}m\ne2\right)\)
\(\Rightarrow y'=\frac{m-5}{m-2}\)
Để A thuộc góc phần tư thứ nhất thì \(\left\{{}\begin{matrix}x'>0\\y'>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\frac{-1-m}{m-2}>0\left(1\right)\\\frac{m-5}{m-2}>0\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow-1< m< 2\)
\(\left(2\right)\Leftrightarrow\left[{}\begin{matrix}m>5\\m< 2\end{matrix}\right.\)
Ta thấy (1) thoả mãn (2) và thoả mãn m \(\ne2\)
Kl: -1<m<2
Đáp án: B
M cách N một khoảng ngắn nhất khi M là hình chiếu vuông góc của N lên d
Gọi d’ là đường thẳng đi qua N và vuông góc với d. Khi đó, d’ đi qua N và nhận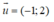 làm vecto pháp tuyến
làm vecto pháp tuyến
d': -(x - 2) + 2(y - 0) = 0 ⇔ -x + 2y + 2 = 0
Suy ra, M là giao điểm của d và d’
Vì M ∈ d ⇒ M(-1-t; 2t)
Vì M ∈ d'⇒ -(-1 - t) + 2.2t + 2 = 0 ⇔ 1 + t + 4t + 2 = 0