Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Vì M nằm trên <> nen M(2t+2;t+3)
Theo đề, ta có: MA=5
\(\Leftrightarrow\sqrt{\left(0-2t-2\right)^2+\left(t+3-1\right)^2}=5\)
\(\Leftrightarrow4t^2+8t+4+t^2+4t+4=25\)
\(\Leftrightarrow5t^2+12t-17=0\)
=>(5t+17)(t-1)=0
=>t=1 hoặc t=-17/5
b:
Đặt (d) là <>
Vì <> có phương trìh tham số là x=2t+2 và y=t+3 nên (d) có vtcplà (2;2) và đi qua điểm A(2;3)
=>VTPT là (-1;1)
Phương trình tổng quát là:
-1(x-2)+1(y-3)=0
=>-x+2+y-3=0
=>-x+y-1=0
=>x-y+1=0
Tọa dộ điểm N là:
\(\left\{{}\begin{matrix}x-y=-1\\x+y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-1\end{matrix}\right.\)
Câu 2:
c/ DO M thuộc \(\Delta\) nên tọa độ M có dạng \(M\left(a;\frac{1-3a}{2}\right)\)
Áp dụng công thức khoảng cách:
\(\frac{\left|5a-\frac{3\left(1-3a\right)}{2}+2\right|}{\sqrt{5^2+3^2}}=5\)
\(\Leftrightarrow\left|13a+1\right|=10\sqrt{34}\)
\(\Leftrightarrow\left[{}\begin{matrix}13a+1=10\sqrt{34}\\13a+1=-10\sqrt{34}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}a=\frac{-1+10\sqrt{34}}{13}\\a=\frac{-1-10\sqrt{34}}{13}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}M\left(\frac{-1+10\sqrt{34}}{13};\frac{8-15\sqrt{34}}{13}\right)\\M\left(\frac{-1-10\sqrt{34}}{13};\frac{8+15\sqrt{34}}{13}\right)\end{matrix}\right.\)
d/ Chẳng hiểu đề câu d là gì luôn? Cái gì bằng 2 lần khoảng cách từ N đến d bạn
Câu 2:
a/ Khoảng cách:
\(d\left(A;\Delta\right)=\frac{\left|3.5+2.4-1\right|}{\sqrt{3^2+2^2}}=\frac{22\sqrt{13}}{13}\)
b/ Gọi \(M\left(x;y\right)\) là 1 điểm thuộc đường phân giác
\(\Rightarrow d\left(M;\Delta\right)=d\left(M;d\right)\)
\(\Rightarrow\frac{\left|3x+2y-1\right|}{\sqrt{3^2+2^2}}=\frac{\left|5x-3y+2\right|}{\sqrt{5^2+3^2}}\)
\(\Leftrightarrow\sqrt{34}\left|3x+2y-1\right|=\sqrt{13}\left|5x-3y+2\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{34}\left(3x+2y-1\right)=\sqrt{13}\left(5x-3y+2\right)\\\sqrt{34}\left(3x+2y-1\right)=-\sqrt{13}\left(5x-3y+2\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(3\sqrt{34}-5\sqrt{13}\right)x+\left(2\sqrt{34}+3\sqrt{13}\right)y-\sqrt{34}-2\sqrt{13}=0\\\left(3\sqrt{34}+5\sqrt{13}\right)x+\left(2\sqrt{34}-3\sqrt{13}\right)y-\sqrt{34}+2\sqrt{13}=0\end{matrix}\right.\)
a: Vì M nằm trên <> nen M(2t+2;t+3)
Theo đề, ta có: MA=5
\(\Leftrightarrow\sqrt{\left(0-2t-2\right)^2+\left(t+3-1\right)^2}=5\)
\(\Leftrightarrow4t^2+8t+4+t^2+4t+4=25\)
\(\Leftrightarrow5t^2+12t-17=0\)
=>(5t+17)(t-1)=0
=>t=1 hoặc t=-17/5
b:
Đặt (d) là <>
Vì <> có phương trìh tham số là x=2t+2 và y=t+3 nên (d) có vtcplà (2;2) và đi qua điểm A(2;3)
=>VTPT là (-1;1)
Phương trình tổng quát là:
-1(x-2)+1(y-3)=0
=>-x+2+y-3=0
=>-x+y-1=0
=>x-y+1=0
Tọa dộ điểm N là:
\(\left\{{}\begin{matrix}x-y=-1\\x+y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-1\end{matrix}\right.\)
bn cho mình gửi sắp đến thi học kì 2 rồi. đây là những món quà mà bn sẽ nhận đc:
1: áo quần
2: tiền
3: đc nhiều người yêu quý
4: may mắn cả
5: luôn vui vẻ trong cuộc sống
6: đc crush thích thầm
7: học giỏi
8: trở nên xinh đẹp
phật sẽ ban cho bn những điều này nếu cậu gửi tin nhắn này cho 25 người, sau 3 ngày bn sẽ có những đc điều đó. nếu bn ko gửi tin nhắn này cho 25 người thì bn sẽ luôn gặp xui xẻo, học kì 2 bn sẽ là học sinh yếu và bạn bè xa lánh( lời nguyền sẽ bắt đầu từ khi đọc) ( mình
cũng bị ép);-;
a/ CD qua E và vuông góc BC nên pt có dạng:
\(1\left(x-6\right)-1\left(y-0\right)=0\Leftrightarrow x-y-6=0\)
Ta có: \(AB=d\left(A;BC\right)=\frac{\left|3+5-2\right|}{\sqrt{1^2+1^2}}=3\sqrt{2}\)
\(AD=d\left(A;CD\right)=\frac{\left|3-5-6\right|}{\sqrt{1^2+\left(-1\right)^2}}=4\sqrt{2}\)
\(\Rightarrow S_{ABCD}=AB.AD=24\)
b/ Do M thuộc d nên tọa độ có dạng: \(M\left(1+t;2-3t\right)\)
Áp dụng công thức khoảng cách:
\(d\left(M;\Delta\right)=4\Leftrightarrow\frac{\left|3\left(1+t\right)+4\left(2-3t\right)+5\right|}{\sqrt{3^2+4^2}}=4\)
\(\Leftrightarrow\left|16-9t\right|=20\Rightarrow\left[{}\begin{matrix}16-9t=20\\16-9t=-20\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}t=-\frac{4}{9}\\t=4\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}M\left(\frac{5}{9};\frac{10}{3}\right)\\M\left(5;-10\right)\end{matrix}\right.\)
Đường thẳng d có phương trình dạng chính tắc: \(\frac{x+2}{-1}=\frac{y-3}{4}\)
\(\Rightarrow\) d đi qua điểm \(M\left(-2;3\right)\)
d nhận \(\left(-1;4\right)\) là 1 vtcp
\(\Rightarrow\) d nhận \(\left(4;1\right)\) là 1 vtpt
b/ Phương trình tham số d: \(\left\{{}\begin{matrix}x=-2-t\\y=3+4t\end{matrix}\right.\)
Hệ số góc: \(k=\frac{4}{-1}=-4\)
Câu 2:
Phương trình đoạn chắn của \(\Delta\): \(\frac{x}{2}+\frac{y}{-6}=1\)
Đáp án: B
M cách N một khoảng ngắn nhất khi M là hình chiếu vuông góc của N lên d
Gọi d’ là đường thẳng đi qua N và vuông góc với d. Khi đó, d’ đi qua N và nhận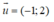
làm vecto pháp tuyến
d': -(x - 2) + 2(y - 0) = 0 ⇔ -x + 2y + 2 = 0
Suy ra, M là giao điểm của d và d’
Vì M ∈ d ⇒ M(-1-t; 2t)
Vì M ∈ d'⇒ -(-1 - t) + 2.2t + 2 = 0 ⇔ 1 + t + 4t + 2 = 0