Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn C.
Không mất tính tổng quát ta gọi 4 nghiệm của phương trình là:
z1= 1; z2= - 2; z3= 1+ i và z4 = 1 - i
Thay vào biểu thức
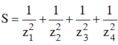
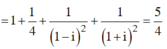
Áp dụng hệ thức Vi-et , ta có \(\begin{cases}z_1+z_2=-b\\z_1.z_2=c\end{cases}\)
Chọn C.
Gọi z = a + bi là nghiệm của phương trình.
Ta có: 4(a + bi) 2 + 8(a2 + b2) - 3 = 0
4(a2 – b2 + 2abi) + 8( a2 + b2) - 3 = 0
12a2 + 4b2 +8abi - 3 = 0
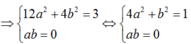
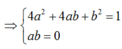
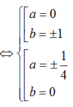
Vậy phương trình có 4 nghiệm phức.
Chọn D.
Phương trình đã cho tương đương với phương trình
z( z + 2) ( z - 1) ( z + 3)
Hay ( z2 + 2z) ( z2 + 2z - 3) = 10
Đặt t = z2 + 2z. Khi đó phương trình trở thành: t2 - 2t – 10 = 0.
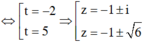
Vậy phương trình có các nghiệm: 
Tổng tất cả các phần thực của các nghiệm phương trình đã cho là:
-1+ ( -1) + (-1) + ( -1) = -4.
Chọn C