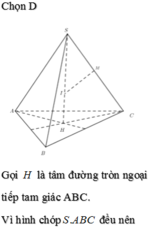
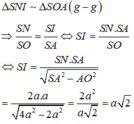Bán kính của mặt cầu ngoại tiếp hình chóp đều S.ABC có tất cả các cạnh bằng a là ...
Đọc tiếp
Bán kính của mặt cầu ngoại tiếp hình
chóp đều S.ABC có tất cả các cạnh
bằng a là
K
Khách
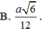
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
18 tháng 5 2017
Đúng(0)
Những câu hỏi liên quan
CM
12 tháng 5 2018
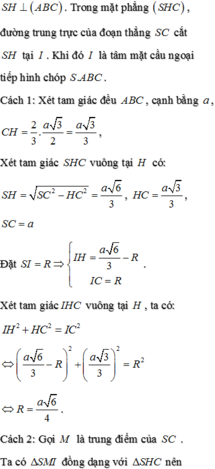
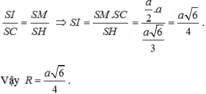
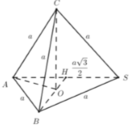
Ta có C A = C B = C S = a Hình chiếu của C trên (SAB) trùng với tâm đường tròn ngoại tiếp ∆ S A B .
Gọi O là tâm đường tròn ngoại tiếp ∆ S A B ⇒ S O ⊥ S A B .
Gọi H là trung điểm của SA. Tam giác SAB cân tại B ⇒ B H ⊥ S A ⇒ O ∈ B H .
Ta có:
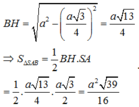
Gọi R là bán kính ngoại tiếp
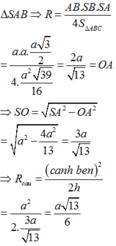
Chọn D.
CM
31 tháng 12 2017
Chọn C.
Phương pháp:
Xác định tâm mặt cầu ngoại tiếp hình chóp đều là giao của đường trung trực 1 cạnh bên và chiều cao của hình chóp.
Từ đó sử dụng tam giác đồng dạng để tính bán kính mặt cầu ngoại tiếp hình chóp đều.
Cách giải:
CM
28 tháng 5 2018
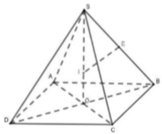
Chon B.
Phương pháp:
Xác định trục của khối chóp sau đó dựng đường thẳng trung trực của một cạnh bên của khối chóp để tìm được tâm của mặt cầu. Từ đó tính bán kính mặt cầu.
Cách giải:
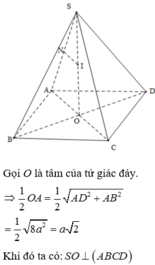
=>SO là trục của đường tròn ngoại tiếp tứ giác ABCD.
Trong mặt phẳng (SOA), vẽ đường trung trực của cạnh SA, cắt SO tại I.
=>I là tâm mặt cầu ngoại tiếp hình chóp.
Ta có:
