Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn C.
Phương pháp: Sử dụng phép biến hình.
Cách giải: Giả sử M, N là điểm biểu diễn số phức z 1 , z 2 theo giả thiết suy ra M, N nằm trên đường tròn tâm I(5;3) bán kính r = 5 và MN là dây cung có độ dài bằng 8. Do đó
trung điểm A của MN nằm trên đường tròn tâm I bán kính r' = 3.
Giả sử M, N là điểm biểu diễn số phức z 1 , z 2 theo giả thiết suy ra M, N nằm trên đường tròn tâm I(5;3) bán kính r = 5 và MN là dây cung có độ dài bằng 8. Do đó trung điểm A của MN nằm trên đường tròn tâm I bán kính r' = 3.
Chọn C.
Chọn C.
Phương pháp: Biến đổi đẳng thức đã cho.
Cách giải: Giả sử
Vậy tập hợp tất cả các điểm biểu diễn số phức z thỏa mãn điều kiện z - i = 2 - 3 i - z là một đường thẳng.
Đáp án D.
Gọi M là điểm biểu diễn của số phức z. Xét điểm A(-1;3) thì theo điều kiện, ta có: 
Vậy tập hợp các điểm biểu diễn z là phần hình phẳng nằm giữa 2 đường tròn tâm A, bán kính lần lượt là 3 và 5
Đáp án D.
Gọi M là điểm biểu diễn của số phức z. Xét điểm A − 1 ; 3 thì theo điều kiện, ta có: 3 ≤ z − 3 i + 1 ≤ 5 ⇔ 3 ≤ A M ≤ 5. Vậy tập hợp các điểm biểu diễn z là phần hình phẳng nằm giữa 2 đường tròn tâm A, bán kính lần lượt là 3 và 5
⇒ S = π 5 2 − 3 3 = 16 π .
Đáp án D.
Gọi M là điểm biểu diễn của số phức z. Xét điểm A(-1;3) thì theo điều kiện, ta có
Vậy tập hợp các điểm biểu diễn z là phần hình phẳng nằm giữa 2 đường tròn tâm A, bán kính lần lượt là 3 và 5
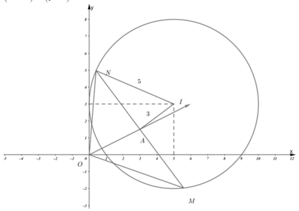
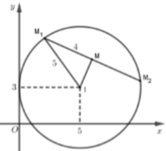
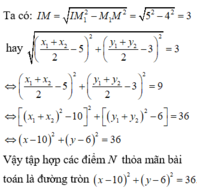
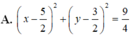
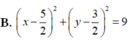
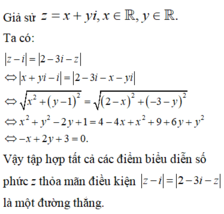
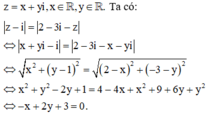
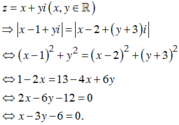
Tập hợp điểm biểu diễn số phức z=x+yi thỏa mãn |z-5-3i|=5 là đường tròn tâm I(5;3) bán kính R=5
Gọi M 1 ( x 1 ; y 1 ) ; M 2 ( x 2 ; y 2 ) là hai điểm biểu diễn các số phức z 1 ; z 2 thì từ z 1 - z 2 = 8 ta suy ra M 1 M 2 = 8
Gọi N(x;y) là điểm biểu diễn số phức w = z 1 + z 2 thì x = x 1 + x 2 y = y 1 + y 2
Gọi M là trung điểm M 1 M 2 thì M x 1 + x 2 2 ; y 1 + y 2 2
Ta có:
hay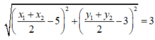
Vậy tập hợp các điểm N thỏa mãn bài toán là đường tròn
Chọn đáp án A.