Cho đồ thị C : x 3 − 3 x 2 . Có bao nhiêu số nguyên b ∈ − 10 ; 10 để có đúng một tiếp tuyến của (C) đi qua điểm B(0;b)
A. 17
B. 9
C. 2
D. 16
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lần lượt thay tọa độ các điểm M, O, P, Q, A vào hàm số f ( x ) = 3 x ta được:
+) Với M (1; 1), thay x = 1 ; y = 1 ta được 1 = 3 . 1 ⇔ 1 = 3 (vô lý) nên M ∉ (C)
+) Với O (0; 0), thay x = 0 ; y = 0 ta được 0 = 3 . 0 ⇔ 0 = 0 (luôn đúng) nên O ∈ (C)
+) Với P (−1; −3), thay x = − 1 ; y = − 3 ta được − 3 = 3 . ( − 1 ) ⇔ − 3 = − 3 (luôn đúng) nên P ∈ (C)
+) Với Q (3; 9), thay x = 3 ; y = 9 ta được 9 = 3 . 3 ⇔ 9 = 9 (luôn đúng) nên Q ∈ (C)
+) Với M (−2; 6), thay x = − 2 ; y = 6 ta được 6 = 3 . ( − 2 ) ⇔ 6 = − 6 (vô lý) nên A (C)
Vậy có ba điểm thuộc đồ thị (C) trong số các điểm đã cho.
Đáp án cần chọn là: B

a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-b}{2a}=\dfrac{-1}{2}\\y=-\dfrac{b^2-4ac}{4a}=-\dfrac{1^2-4\cdot1\cdot\left(-2\right)}{4\cdot1}=-\dfrac{1+8}{4}=-\dfrac{9}{4}\end{matrix}\right.\)
Vì (P): \(y=x^2+x-2\) có a=1>0
nên (P) đồng biến khi x>-1/2 và nghịch biến khi x<-1/2
Vẽ (P): 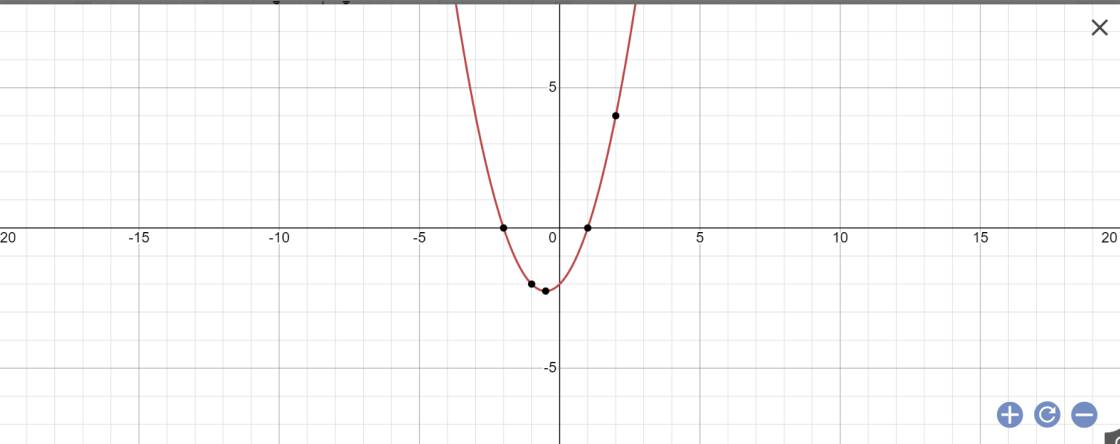
b: Phương trình hoành độ giao điểm là:
\(x^2+x-2=-\left(m+1\right)x+m+2\)
=>\(x^2+x-2+\left(m+1\right)x-m-2=0\)
=>\(x^2+\left(m+2\right)x-m-4=0\)(1)
Để (P) cắt (d) tại hai điểm phân biệt A,B nằm về hai phía so với trục Oy thì phương trình (1) có hai nghiệm phân biệt trái dấu
=>-m-4<0
=>-m<4
=>m>-4
mà \(m\in Z;m\in\left[-10;4\right]\)
nên \(m\in\left\{-3;-2;-1;0;1;2;3;4\right\}\)
=>Có 8 số thỏa mãn
Đáp án là A