Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Hàm số đã cho là y = 2x + b.
Vì đồ thị đi qua điểm A(1,5; 0) nên 0 = 2 . 1,5 + b. Suy ra b = -3.
Vậy hàm số đã cho là y = 2x - 3.
b) Hàm số đã cho là y = 3x + b.
Vì đồ thị đi qua điểm A(2; 2) nên 2 = 3 . 2 + b. Suy ra b = -4.
Vậy hàm số đã cho là y = 3x - 4.
c) Vì đồ thị của hàm số đã cho song song với đường thẳng y = √3x nên nó có hệ số góc là a = √3. Do đó hàm số đã cho là y = √3x + b.
Vì đồ thị đi qua điểm B(1; √3 + 5) nên √3 + 5 = √3 . 1 + b. Suy ra b = 5.
Vậy hàm số đã cho là y = √3x + 5.
Bài giải:
a) Hàm số đã cho là y = 2x + b.
Vì đồ thị đi qua điểm A(1,5; 0) nên 0 = 2 . 1,5 + b. Suy ra b = -3.
Vậy hàm số đã cho là y = 2x - 3.
b) Hàm số đã cho là y = 3x + b.
Vì đồ thị đi qua điểm A(2; 2) nên 2 = 3 . 2 + b. Suy ra b = -4.
Vậy hàm số đã cho là y = 3x - 4.
c) Vì đồ thị của hàm số đã cho song song với đường thẳng y = √3x nên nó có hệ số góc là a = √3. Do đó hàm số đã cho là y = √3x + b.
Vì đồ thị đi qua điểm B(1; √3 + 5) nên √3 + 5 = √3 . 1 + b. Suy ra b = 5.
Vậy hàm số đã cho là y = √3x + 5
Điều kiện xác định: \(x\ge0\).
Lấy \(x_1>x_2\ge0\).
\(f\left(x_1\right)-f\left(x_2\right)=\sqrt{x_1}-\sqrt{x_2}=\frac{x_1-x_2}{\sqrt{x_1}+\sqrt{x_2}}>0\)
Do đó hàm số đồng biến.
Lần lượt thế tọa độ các điểm vào hàm số ban đầu, ta thấy điểm \(C\left(9,3\right)\)thỏa mãn nên nó thuộc đồ thị của hàm số đã cho, các điểm khác không thuộc.
a) Vì đồ thị hàm số đi qua A(1;-1) nên ta có :
x= 1 ; y=-1 và thay vào hàm số ta có
y= (2a+3) <=> -1 = (2a + 3)*1 <=> 2a + 3 = -1 <=> 2a = - 3 - 1 <=> 2a = -4 <=> a = -2
Vậy đồ thị hàm số có dạng y = ( -4 +3)x = -1x
- Ta có phương trình hoành độ giao điểm :
-1x = 4x - 5
<=> -1x - 4x = -5
<=>-5x = -5 <=> x = 1 => y = -1x = -1 * 1 = -1
Vậy 2 đồ thị hàm số giao nhau tại B ( 1; -1)
b) Vì hoành độ bằng 1 bằng 1 nên x = 1
Ta có phương trình hoành độ giao điểm :
(2a + 3 )x = -2x +2
thay x = 1 vào phương trình ta có :
( 2a + 3)*1 = -2*1 + 2
<=> 2a + 3 = -2+ 2
<=> 2a = -2 +2 -3 <=> a = \(-\frac{3}{2}\)
Câu 1:
a,Bạn tự vẽ
b,Phương trình hoành độ giao điểm của (d1) và (d2) là:
\(\(\(-2x+3=x-1\Rightarrow-3x=-4\Rightarrow x=\frac{4}{3}\)\)\)
\(\(\(\Rightarrow y=\frac{4}{3}-1=\frac{1}{3}\)\)\)
Vậy tọa độ giao điểm của (d1) và (d2) là \(\(\(\left(\frac{4}{3};\frac{1}{3}\right)\)\)\)
c,Đường thẳng (d3) có dạng: y = ax + b
Vì (d3) song song với (d1) \(\(\(\Rightarrow\hept{\begin{cases}a=a'\\b\ne b'\end{cases}}\Rightarrow\hept{\begin{cases}a=-2\\b\ne3\end{cases}}\)\)\)
Khi đó (d3) có dạng: y = -2x + b
Vì (d3) đi qua điểm A( -2 ; 1) nên \(\(\(\Rightarrow x=-2;y=1\)\)\)
Thay x = -2 ; y = 1 vào (d3) ta được:\(\(\(1=-2.\left(-2\right)+b\Rightarrow b=-3\)\)\)
Vậy (d3) có phương trình: y = -2x - 3
Câu 2:
\(A=\frac{a\sqrt{b}+b\sqrt{a}}{\sqrt{ab}}:\frac{1}{\sqrt{a}-\sqrt{b}}\left(a>0;b>0;a\ne b\right)\)(Đề chắc phải như này)
\(\(\(=\frac{\sqrt{ab}\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{ab}}.\frac{\sqrt{a}-\sqrt{b}}{1}\)\)\)
\(\(\(=\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)\)\)\)
\(\(\(=\sqrt{a}^2-\sqrt{b}^2\)\)\)
\(\(\(=a-b\)\)\)
a: Thay x=-2 và y=b vào (P), ta được:
\(b=\left(-2\right)^2\cdot0.2=0.8\)
Vì trong (P) thì f(x)=f(-x)
nên A'(2;0,8) thuộc (P)
b: Thay x=c và y=6 vào (P), ta được:
\(0,2c^2=6\)
nên \(c=\sqrt{30}\)
Vì trong (P) thì f(x)=f(-x) nên \(D\left(\sqrt{30};-6\right)\in\left(P\right)\)
Bài giải:
Vẽ đồ thị: y = 
x2
|
x |
-6 |
-3 |
0 |
3 |
6 |
|
y = |
12 |
3 |
0 |
3 |
12 |
y = -x + 6
- Cho x = 0 => y = 6.
- Cho y = 0 => x = 6.
Vẽ đồ thị: xem hình bên dưới.
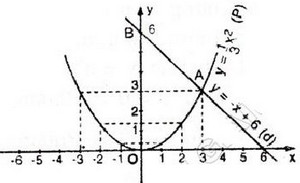
b) Giá trị gần đúng của tọa độ câc giao điểm (thực ra đây là giá trị đúng).
Hai đồ thị cắt nhau tại hai điểm A và B.
Theo đồ thị ta có A(3; 3) và B(-6; 12).
Lần lượt thay tọa độ các điểm M, O, P, Q, A vào hàm số f ( x ) = 3 x ta được:
+) Với M (1; 1), thay x = 1 ; y = 1 ta được 1 = 3 . 1 ⇔ 1 = 3 (vô lý) nên M ∉ (C)
+) Với O (0; 0), thay x = 0 ; y = 0 ta được 0 = 3 . 0 ⇔ 0 = 0 (luôn đúng) nên O ∈ (C)
+) Với P (−1; −3), thay x = − 1 ; y = − 3 ta được − 3 = 3 . ( − 1 ) ⇔ − 3 = − 3 (luôn đúng) nên P ∈ (C)
+) Với Q (3; 9), thay x = 3 ; y = 9 ta được 9 = 3 . 3 ⇔ 9 = 9 (luôn đúng) nên Q ∈ (C)
+) Với M (−2; 6), thay x = − 2 ; y = 6 ta được 6 = 3 . ( − 2 ) ⇔ 6 = − 6 (vô lý) nên A (C)
Vậy có ba điểm thuộc đồ thị (C) trong số các điểm đã cho.
Đáp án cần chọn là: B