Có bao nhiêu giá trị của tham số m để đồ thị hàm số y = mx + x 2 - 2 x + 3 2 x - 1 có một tiệm cận ngang là y = 2.
A. 1.
B. 2.
C. 0.
D. vô số.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Ta có:
![]()
nên đồ thị hàm số luôn có 1 TCN là y = 0
Đồ thị hàm số có 2 đường tiệm cận thì nó chỉ có duy nhất 1 đường tiệm cận đứng
⇔ phương trình x 2 + m x + 4 = 0 có nghiệm x = 1
hoặc phương trình x 2 + m x + 4 = 0 có nghiệm kép (có thể bằng 1)

Vậy có 3 giá trị của m thỏa mãn bài toán

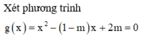
Đồ thị hàm số đã cho có 2 đường tiệm cận đứng ⇔ phương trình g(x) có 2 nghiệm phân biệt

Đáp án C
Yêu cầu bài toán ⇔ x 2 - ( 1 - m ) x + 2 m = 0 có 2 nghiệm phân biệt lớn hơn hoặc bằng -1
Khi và chỉ khi ∆ > 0 x 1 + x 2 + 2 ≥ 0 x 1 + 1 x 2 + 1 ≥ 0 ⇔ 1 - m 2 - 4 . 2 m > 0 1 - m + 2 ≥ 0 2 m + 2 - m + 1 ≥ 0 ⇔ - 2 ≤ m ≤ 5 - 2 6 .

- Với \(m=0\Rightarrow y=-x^2-2\) chỉ có cực đại (thỏa mãn)
- Với \(m\ne0\) hàm chỉ có cực đại khi:
\(\left\{{}\begin{matrix}m< 0\\m\left(2m-1\right)\ge0\end{matrix}\right.\) \(\Leftrightarrow m< 0\)
Vậy \(m\le0\)

Hàm số g(x) nghịch biến trên khoảng (0;1) khi ![]()
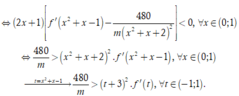
Dựa vào đồ thị, ta có
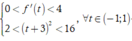
![]()
Theo YCBT 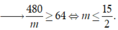
Chọn C.
Chọn B.