Thế nào là hệ số biến dạng?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 10 2019
+ Phép biến hình trong mặt phẳng là quy tắc đặt tương ứng mỗi điểm M trong mặt phẳng xác định được duy nhất M’ trong mặt phẳng đó.
+ Phép dời hình là phép biến hình bảo toàn khoẳng cách giữa hai điểm bất kì.
+ Phép đồng dạng tỉ số k là phép biến hình biến hai điểm M, N bất kì thành M’; N’ sao cho M’N’ = k.MN.
+ Phép dời hình chính là phép đồng dạng với tỉ số k = 1.
Q
31 tháng 3 2017
- Phép biến hình:
Quy tắc đặt tương ứng mỗi điểm M của mặt phẳng với một điểm xác định duy nhất M\' của mặt phẳng đó được gọi là phép biến hình trong mặt phẳng. Nếu kí hiệu phép biến hình đó là F thì ta viết F(M) = M\' hay M\' = F(M) và gọi điểm M\' là ảnh của điểm M hay M là điểm tạo ảnh của M\' qua phép biến hình F.
- Phép dời hình:
Phép dời hình là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kì. Nghĩa là với hai điểm M, N tùy ý và ảnh M', N' tương ứng của chúng, ta luôn có M'N'=MN.
- Phép đồng dạng:
Phép biến hình f được gọi là phép đồng dạng tỉ số k, (k>0), nếu với hai điểm M, N bất kì và ảnh M\', N\' tương ứng của chúng, ta luôn có M\'N\' = kMN.
Mối liên hệ: Phép dời hình là trường hợp riêng của phép đồng dạng với tỉ số k = 1.
31 tháng 3 2017
- Phép biến hình:
Quy tắc đặt tương ứng mỗi điểm M của mặt phẳng với một điểm xác định duy nhất M\' của mặt phẳng đó được gọi là phép biến hình trong mặt phẳng. Nếu kí hiệu phép biến hình đó là F thì ta viết F(M) = M' hay M' = F(M) và gọi điểm M' là ảnh của điểm M hay M là điểm tạo ảnh của M\' qua phép biến hình F.
- Phép dời hình:
Phép dời hình là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kì. Nghĩa là với hai điểm M, N tùy ý và ảnh M', N' tương ứng của chúng, ta luôn có M'N'=MN.
- Phép đồng dạng:
Phép biến hình f được gọi là phép đồng dạng tỉ số k, (k>0), nếu với hai điểm M, N bất kì và ảnh M', N' tương ứng của chúng, ta luôn có M'N' = kMN.
Mối liên hệ: Phép dời hình là trường hợp riêng của phép đồng dạng với tỉ số k = 1.
MH
28 tháng 12 2020
Câu 1:
Kì trung gian | Kì đầu | Kì giữa | Kì sau | Kì cuối | |
Số NST đơn | 0 | 0 | 0 | 4n | 2n |
Sô NST kép | 2n | 2n | 2n | 0 | 0 |
MH
28 tháng 12 2020
Câu 2:
– Tính đặc thù của ADN do số lượng, thành phần và đặc biệt là trình tự sắp xếp của các nuclêôtit. Những cách sắp xếp khác nhau của các loại nucleotit tạo nên tính đa dạng của ADN.
– Tính đa dạng và đặc thù của ADN được chi phối chủ yếu do ADN cấu trúc theo nguyên tắc đa phân với 4 loại đơn phân: A, T, G, X.
KN
1
4 tháng 11 2019
Các loại biến dạng của rễ:
- Rễ củ: chứa chất dự trữ cho cây khi ra hoa, tạo quả.
Vd: củ cà rốt ,cây cải củ,..
- Rễ móc : bám vào trụ giúp cây leo lên.
Vd: cây trầu không,.
- Rễ thở : giúp cây hô hấp trong không khí
Vd: cây bụt moc,...
- Giác mút : lấy thức ăn từ vật chủ
Vd: dây tơ hồng, cây tầm gửi,..
* Các loại thân biến dạng:
- Thân củ :khoai tây, su hào, gừng,..
- Thân rễ : giềng, nghệ, dong ta,..
- Thân mọng nước : cây xương rồng, cây cành giao, cây thuốc bỏng,..
cho nhé
13 tháng 12 2021
1.
TK:
- Đột biến số lượng NST là những biến đổi về số lượng NST xảy ra ở 1 hoặc 1 số cặp NST tương đồng (đột biến dị bội - lệch bội) hoặc xảy ra ở tất cả các cặp NST (đột biến đa bội). - Đột biến số lượng NST bao gồm: + Đột biến lệch bội. + Đột biến đa bội: tự đa bội (chẵn và lẻ), dị đa bội.
DT
14 tháng 12 2021
tk:
- Đột biến số lượng NST là những biến đổi về số lượng NST xảy ra ở 1 hoặc 1 số cặp NST tương đồng (đột biến dị bội - lệch bội) hoặc xảy ra ở tất cả các cặp NST (đột biến đa bội). - Đột biến số lượng NST bao gồm: + Đột biến lệch bội. + Đột biến đa bội: tự đa bội (chẵn và lẻ), dị đa bội.
NK
14 tháng 12 2021
1.- Đột biến số lượng NST là những biến đổi về số lượng NST xảy ra ở 1 hoặc 1 số cặp NST tương đồng (đột biến dị bội - lệch bội) hoặc xảy ra ở tất cả các cặp NST (đột biến đa bội).
Ví dụ: Ở người Nếu cá thể có 3 NST 21 => bị bệnh Đao: là thể lệch bội.
VT
23 tháng 11 2019
Độ biến dạng của lò xo là hiệu giữa chiều dài khi biến dạng và chiều dài tự nhiên của lò xo.
Kí hiệu độ biến dạng là ∆ l (đọc là đenta l ).
Công thức tính độ biến dạng: ∆ l = l – l 0
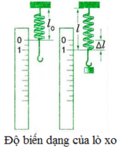
Chú ý: Khi lò xo bị biến dạng nén thì độ biến dạng là hiệu độ dài tự nhiên và độ dài của lò xo khi bị nén.
Hệ số biến dạng là tỉ số độ dài hình chiếu của một đoạn thẳng nằm trên trục toạ độ với độ dài thực của đoạn thẳng đó. Thông thường có 3 hệ số biến dạng chính là: Hệ số biến dạng theo trục O’X’, hệ số biến dạng O’Y’, hệ số biến dạng O’Z’.