Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn C
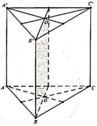
Hình lăng trụ đứng có đáy là tam giác cân nhưng không phải là tam giác đều có 2 mặt phẳng đối xứng gồm mặt phẳng trung trực của cạnh bên và mặt phẳng trung trực của cạnh đáy của tam giác đáy hình lăng trụ (hình vẽ minh họa).
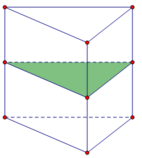
Đáp án A.
Vì A ’ A = A ’ B = A ’ C ⇒ A ' . A B C là hình chóp tam giác đều.
Hình vẽ minh họa: Hình chóp tam giác đều ABCD có 3 mặt phẳng đối xứng.
Vậy hình chóp tam giác đều (không phải tứ diện đều) có 3 mặt phẳng đối xứng.
a) Đáy của hình lăng trụ đứng là một tam giác vuông cân
b) Các mặt bên nhận được không phải tất cả là hình vuông
\(\Bigg(\) hai hình vuông và một hình chữ nhật \(\Bigg)\)
Đáp án A.
Hướng dẫn giải:
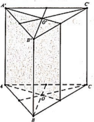
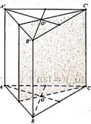
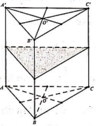
Hình lăng trụ tam giác đều có 4 mặt phẳng đối xứng (Hình vẽ bên dưới)
Chọn đáp án D
Hình lăng trụ tam giác đều có 4 mặt phẳng đối xứng
Chọn đáp án D
Hình lăng trụ tam giác đều có 4 mặt phẳng đối xứng
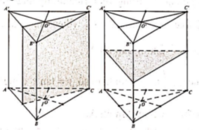
Đáp án C
Có 2 mặt phẳng đối xứng là mặt phẳng vuông góc với đáy và đi qua đường cao ứng với cạnh đáy của đáy và mặt phẳng song song với đáy đi qua trung điểm của cạnh bên hình lăng trụ