Cho tam giác ABC cân tại A với ∠ A = 70 o , AI là tia phân giác của góc BAC. Khi đó số đo của góc BAI là:
A. 50 °
B. 45 °
C. 35 °
D. 30 °
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 8 2019
Vì tam giác ABC đều nên (BAC) ̂=60^0.
AI là tia phân giác của góc BAC nên (BAI) ̂=30^0. Chọn A
6 tháng 4 2022
a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
b: \(\widehat{ABC}=\dfrac{180^0-30^0}{2}=75^0\)
c: Xét tứ giác AHCE có
D là trung điểm của AC
D là trung điểm của HE
Do đó: AHCE là hình bình hành
Suy ra: AH//CE
TT
15 tháng 5 2021
b) Xét ΔADH và ΔCDE có
Góc ADH = Góc EDC ( đối đỉnh )
D là tđ của HE => HD=ED
D là tđ của AC => AD=DC
=>ΔADH = ΔCDE (cgc)
=> góc DAH = góc ECD ( 2 góc tương ứng )
mà 2 góc trên ở vị trí so le trong
=>HA// EC
Xét ΔAHC có
F là tđ của AH => CF là trung tuyến
D là tđ của AC => HD là trung tuyến
mà CF giao vs HD tại Q => Q là trọng tâm
=> HQ=\(\dfrac{2}{3}\)HD
mà HD=DE (cmt)
=>HQ=\(\dfrac{HD+DE}{3}\)=\(\dfrac{1}{3}HE\)
thế là xong câu b rùi nhé còn còn a thì dễ r bạn tự làm đc 
CM
10 tháng 5 2018
Ta có AI là tia phân giác của góc A nên ∠(BAI) = 40o:2=20o. Chọn A
CM
18 tháng 2 2017
Ta có AI là tia phân giác của góc A nên ∠(BAI) = 40o:2=20o. Chọn A
17 tháng 9 2023
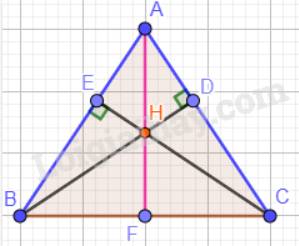
a) Tam giác ABC cân tại A nên: \(\widehat {ABC} = \widehat {ACB} = 70^\circ \).
Tổng ba góc trong một tam giác bằng 180° nên: \(\widehat {BAC} = 180^\circ - 70^\circ - 70^\circ = 40^\circ \).
b) Xét tam giác vuông ADB và tam giác vuông AEC có:
AB = AC (tam giác ABC cân);
\(\widehat A\) chung.
Vậy \(\Delta ADB = \Delta AEC\)(cạnh huyền – góc nhọn). Suy ra: BD = CE ( 2 cạnh tương ứng).
c) Trong tam giác ABC có H là giao điểm của hai đường cao BD và CE nên H là trực tâm trong tam giác ABC hay AF vuông góc với BC.
Xét hai tam giác vuông AFB và AFC có:
AB = AC (tam giác ABC cân);
AF chung.
Vậy \(\Delta AFB = \Delta AFC\)(cạnh huyền – cạnh góc vuông). Suy ra: \(\widehat {FAB} = \widehat {FAC}\) ( 2 góc tương ứng) hay \(\widehat {BAH} = \widehat {CAH}\).
Vậy tia AH là tia phân giác của góc BAC.
Số đo của góc BAI là 70 : 2 = 35o. Chọn C