Cho tứ diện đều ABCD cạnh a. Thể tích của khối tứ diện ABCD là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

.png)
Gọi \(M\) là trung điểm của \(BC\), \(O\) là trọng tâm tam giác \(ABC\).
\( \Rightarrow SO \bot \left( {ABC} \right)\)
Tam giác \(ABC\) đều
\( \Rightarrow AM = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2} \Rightarrow AO = \frac{2}{3}AM = \frac{{a\sqrt 3 }}{3}\)
Tam giác \(SAO\) vuông tại \(O \Rightarrow SO = \sqrt {S{A^2} - A{O^2}} = \frac{{a\sqrt 6 }}{3}\)
\(\begin{array}{l}{S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4}\\{V_{S.ABC}} = \frac{1}{3}{S_{\Delta ABC}}.SO = \frac{{{a^3}\sqrt 2 }}{{12}}\end{array}\)

Đáp án B
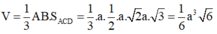
Phương án nhiễu.
A. Sai vì 2 cách: một là thấy số 1 3 cứ chọn, hai là trong công thức thể tích thiếu 1 3 diện tích đáy.
C. Sai vì thiếu 1 3 trong công thức thể tích.

Chọn C
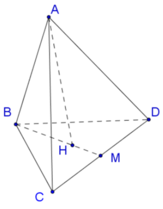
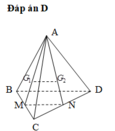
Gọi M là trung điểm của CD, H là trọng tâm của tam giác BCD

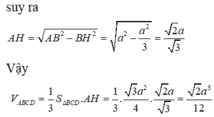

Đáp án B
Gọi M là trung điểm của CD , H là trọng tâm của tam giác BCD.
Ta có AH ⊥ BCD (giả thiết ABCD là tứ diện đều) suy ra

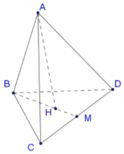


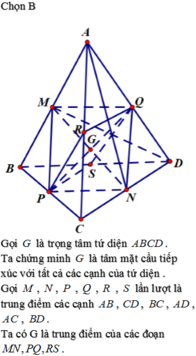

Đáp án C
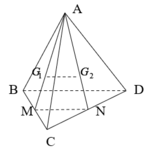
Gọi M là trung điểm của CD, H là trọng tâm của tam giác BCD.
Ta có A H ⊥ B C D (giả thiết ABCD là tứ diện đều)