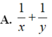
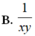
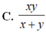
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Ta có log(x + 2y) = log x + log y
<=> log 2 (x+2y) = log 2xy
<=> 2 (x+2y) = 2xy (*).
Đ ặ t a = x > 0 b = 2 y > 0 , khi đó
* ⇔ 2 a + b = a b
và P = a 2 1 + b + b 2 1 + a ≥ a + b 2 a + b + 2
Lại có a b ≤ a + b 2 4 ⇒ 2 a + b ≤ a + b 2 4 ⇔ a + b ≥ 8 .
Đặt t = a + b, do đó
P ≥ f t = t 2 t + 2 .
X é t h à m s ố f t = t 2 t + 2 t r ê n [ 8 ; + ∞ )
c ó f ' t = t 2 + 2 t t + 2 2 > 0 ; ∀ ≥ 8
Suy ra f(t) là hàm số đồng biến trên [ 8 ; + ∞ )
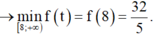
Vậy gía trị nhỏ nhất của biểu thức P là 32 5 .
a) Với \(x = 1\) thì \(y = {\log _2}1 = 0\)
Với \(x = 2\) thì \(y = {\log _2}2 = 1\)
Với \(x = 4\) thì \(y = {\log _2}4 = 2\)
b) Biểu thức \(y = {\log _2}x\) có nghĩa khi x > 0.
\(a,log_a1=c\Leftrightarrow a^c=1\Leftrightarrow c=0\Rightarrow log_a1=0\\ b,log_aa=c\Leftrightarrow a^c=a\Leftrightarrow c=1\Rightarrow log_aa=1\\ c,log_aa^c=b\Leftrightarrow a^b=a^c\Leftrightarrow b=c\Rightarrow log_aa^c=c\\ d,a^{log_ab}=c\Leftrightarrow log_ab=log_ac\Leftrightarrow b=c\Rightarrow a^{log_ab}=b\)
Hàm số \(y=log_cx\) nghịch biến
\(\Rightarrow0< c< 1\) và các hàm \(y=log_ax,y=log_bx\) đồng biến nên \(a,b>1\)
Ta chọn \(x=100\Rightarrow log_a>log_b100\Rightarrow a< b\Rightarrow b>a>c\)
\(\Rightarrow B\)
Khoảng giá trị của x mà đồ thị hàm số \(y=log_2x\) nằm phía trên đường thẳng y = 2 là \(\left(4;+\infty\right)\)
\(\Rightarrow\) Tập nghiệm của bất phương trình \(log_2x>2\) là \(\left(4;+\infty\right)\)
Đáp án C