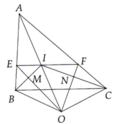
cho tam giác ABC cân tại A. vẽ các đường phân giác AD, BE, CF. đường thẳng đi qua A và song song BC cắt DF và DE tại M và N. a)chứng minh: FE//BC
b) cm : A là trung điểm MN
c) gọi I là giao 3 đường phân giác của tam giác ABC . Tính diện tích BIC . Biết AB=5 , BC=6