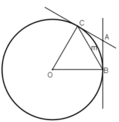
Cho đường tròn (O) và dây BC = 2 R. Hai tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại A. Tính góc A B C ^
A. 45 °
B. 30 °
C. 60 °
D. 75 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác OBA có OB = OC = BC = R
Vậy tam giác OAB là tam giác đều
=> ^BOC = ^OBC = ^OCB = 600
Vì AB ; AC là tiếp tuyến đường tròn (O) với B;C là tiếp điểm
=> ^OBA = ^OCA = 900
=> ^ABC = ^OBA - ^OBC = 900 - 600 = 300
Do AB = AC ( tc tiếp tuyến cắt nhau )
=> ^ABC = ^ACB = 300
=> ^BAC = 1800 - 2^ABC = 1200

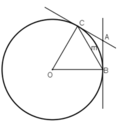
+ ΔOBC có OB = OC = BC (= R)
⇒ ΔOBC là tam giác đều

+ 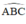 là góc tạo bởi tiếp tuyến BA và dây BC
là góc tạo bởi tiếp tuyến BA và dây BC
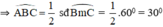
+ 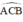 là góc tạo bởi tiếp tuyến AC và dây CB
là góc tạo bởi tiếp tuyến AC và dây CB
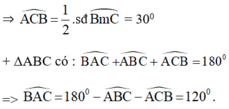

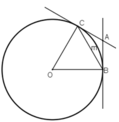
+ ΔOBC có OB = OC = BC (= R)
⇒ ΔOBC là tam giác đều

+ 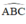 là góc tạo bởi tiếp tuyến BA và dây BC
là góc tạo bởi tiếp tuyến BA và dây BC

+ 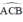 là góc tạo bởi tiếp tuyến AC và dây CB
là góc tạo bởi tiếp tuyến AC và dây CB
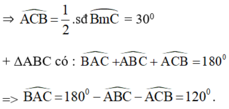
Kiến thức áp dụng
+ Trong một đường tròn, số đo của cung là số đo của góc ở tâm chắn cung đó.
+ Số đo của góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.

+ ΔOBC có OB = OC = BC (= R)
⇒ ΔOBC là tam giác đều

+ 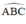 là góc tạo bởi tiếp tuyến BA và dây BC
là góc tạo bởi tiếp tuyến BA và dây BC
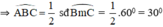
+ 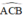 là góc tạo bởi tiếp tuyến AC và dây CB
là góc tạo bởi tiếp tuyến AC và dây CB
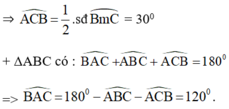

\(ABC\) cân tại A \(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
\(\left\{{}\begin{matrix}\widehat{ACB}+\widehat{BCH}=90^0\\\widehat{CBH}+\widehat{BCH}=90^0\end{matrix}\right.\) \(\Rightarrow\widehat{ACB}=\widehat{CBH}\)
\(\Rightarrow\widehat{ABC}=\widehat{CBH}\)

a: Xét tứ giác ABOC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
=>ABOC là tứ giác nội tiếp
=>A,B,O,C cùng thuộc một đường tròn
b: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại trung điểm K của BC
K là trung điểm của BC
nên \(KB=KC=\dfrac{BC}{2}=12\left(cm\right)\)
Ta có: ΔBKO vuông tại K
=>\(KB^2+KO^2=OB^2\)
=>\(OK^2=15^2-12^2=81\)
=>\(OK=\sqrt{81}=9\left(cm\right)\)
Xét ΔOBA vuông tại B có BK là đường cao
nên \(OK\cdot OA=OB^2\)
=>\(OA=\dfrac{15^2}{9}=25\left(cm\right)\)
Ta có: ΔOBA vuông tại B
=>\(BO^2+BA^2=OA^2\)
=>\(BA^2=25^2-15^2=400\)
=>\(BA=\sqrt{400}=20\left(cm\right)\)
c: Sửa đề: E là giao điểm của AC và BD
Ta có: BH\(\perp\)CD
AC\(\perp\)CD
Do đó: BH//CD
Xét ΔDCA có HI//CA
nên \(\dfrac{HI}{CA}=\dfrac{DI}{DA}\left(3\right)\)
Xét ΔDAE có IB//AE
nên \(\dfrac{IB}{AE}=\dfrac{DI}{DA}\left(4\right)\)
Xét (O) có
ΔDBC nội tiếp
DC là đường kính
Do đó: ΔDBC vuông tại B
=>DB\(\perp\)BC tại B
=>BC\(\perp\)DE tại B
=>ΔCBE vuông tại B
Ta có: \(\widehat{ABE}+\widehat{ABC}=\widehat{CBE}=90^0\)
\(\widehat{AEB}+\widehat{ACB}=90^0\)(ΔCBE vuông tại B)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABE}=\widehat{AEB}\)
=>AB=AE
mà AB=AC
nên AE=AC
Từ (3) và (4) suy ra \(\dfrac{HI}{CA}=\dfrac{IB}{AE}\)
mà CA=AE
nên HI=IB

Chọn đáp án C.
Ta có:
Góc 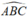 là góc tạo bởi tia tiếp tuyến và dây cung chắn cung BC⌢ nên:
là góc tạo bởi tia tiếp tuyến và dây cung chắn cung BC⌢ nên:

Chọn đáp án A.
Góc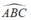 là góc tạo bởi tia tiếp tuyến và dây cung chắn cung BC nên:
là góc tạo bởi tia tiếp tuyến và dây cung chắn cung BC nên: