Hàm số y=sinx đồng biến trên khoảng nào sau đây?
K
Khách
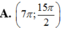
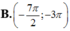
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
11 tháng 1 2018
Đúng(0)
Những câu hỏi liên quan
xác định trên R
30 tháng 5 2021
C1: \(a.sinx+b.cosx=c\)
Pt vô nghiệm \(\Leftrightarrow a^2+b^2< c^2\)
Bạn áp dụng công thức trên sẽ tìm ra m
C2: (Bạn vẽ đường tròn lượng giác sẽ tìm được)
Hàm số \(y=sinx\) đồng biến trên khoảng \(\left(-\dfrac{\pi}{2}+k2\pi;\dfrac{\pi}{2}+k2\pi\right)\) ( góc phần tư thứ IV và I)
Hàm nghịch biến trên khoảng \(\left(\dfrac{\pi}{2}+k2\pi;\dfrac{3\pi}{2}+k2\pi\right)\)( góc phần tư thứ II và III)
Ý A, khoảng nằm trong góc phần tư thứ III và thứ IV => Hàm nghịch biến sau đó đồng biến
Ý B, khoảng nằm trong góc phần tư thứ I và thứ II => hàm đồng biến sau đó nghịch biến
Ý C, khoảng nằm trong góc phần tư thứ IV; I ; II => hàm đồng biền sau đó nghịch biến
Ý D, khoảng nằm trong phần tư thứ IV ; I=> hàm đồng biến
Đ/A: Ý D
(Toi nghĩ thế)
CM
26 tháng 9 2019
Đáp án B
Phương pháp:
Hàm số y = f(x) đồng biến (nghịch biến) trên (a;b) khi và chỉ khi 
và f’(x) = 0tại hữu hạn điểm.
Cách giải:
Quan sát bảng biến thiên, ta thấy: hàm số y = f(x) đồng biến trên khoảng (0;2). Do 
Hàm số y = f(x) đồng biến trên khoảng (0;1)
