

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn B.
Phương pháp : Sử dụng đạo hàm và xét dấu đạo hàm để tìm cực trị.
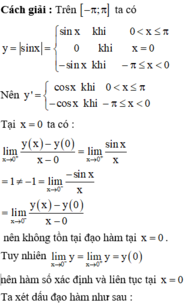
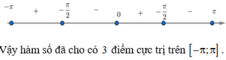

Đáp án B
Phương pháp giải:
Dựa vào đồ thị hàm số xác định hoành độ điểm D suy ra tung độ điểm A chính là độ dài BC
Lời giải: Gọi ![]() với
với ![]()
Gọi ![]() thuộc đồ thị
thuộc đồ thị ![]()
Vì ABCDlà hình chữ nhật ![]()
Khi đó BC = m. Mà ![]()
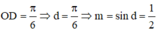

Xét hàm số
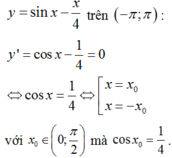
Bảng biến thiên:
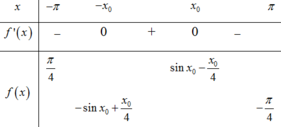
Do y = sin x - x 4 là hàm lẻ nên đồ thị hàm số y = sin x - x 4 nhận O(0;0) là tâm đối xứng.
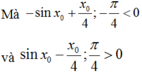
Đồ thị hàm số cắt trục Ox tại 3 điểm phân biệt x 1 ; x 2 ; x 3 ( x 1 ; x 2 ; x 3 khác ± x 0 )
Số điểm cực trị của hàm số số y = sin x - π 4 ; x ∈ - π ; π là: 2 + 2 = 4
Chọn B.

Đáp án C
cos 2 x = − 1 2 = cos 2 π 3 ⇔ 2 x = 2 π 3 + k 2 π 2 x = − 2 π 3 + k 2 π ⇔ x = π 3 + k π x = − π 3 + k π , k ∈ Z
Vì x thuộc − π ; π nên phương trình có hai nghiệm là π 3 và - π 3 .

Đáp án D
Đặt t = cos x ⇒ t ∈ − 1 ; 1 ⇒ y = f t = 2 t + 1 t − m
Ta có f ' t = 2 m + 1 t − m 2 sin x
Hàm số đồng biến trên khoảng:
0 ; π ⇒ f ' t > 0 t − m ≠ 0 ⇔ 2 m + 1 sinx > 0 m ≠ t ⇔ m > − 1 2 m ≥ 1 m ≤ − 1 ⇒ m ≥ 1

Đáp án D
Đặt t = c osx ⇒ t'=-sinx < 0 ; ∀ x ∈ 0 ; π suy ra t ∈ − 1 ; 1 .
Khi đó
y = f t = 2 t + 1 t − m ⇒ f ' t = − 2 m + 1 t − m 2 x t ' .
Hàm số đã cho đồng biến trên khoảng 0 ; π
⇔ f ' t > 0 ; ∀ t ∈ − 1 ; 1 ⇔ − 2 m + 1 t − m 2 x t ' > 0 ; ∀ t ∈ − 1 ; 1
mà t ' < 0 suy ra
2 m + 1 t − m 2 > 0 ; ∀ t ∈ − 1 ; 1 .
⇔ 2 m + 1 > 0 t = m ∉ − 1 ; 1 ⇔ m > − 1 2 m ∉ − 1 ; 1 ⇔ m > − 1 2 1 2 ≥ 1 m ≤ − 1 ⇔ m ≥ 1 là giá trị cần tìm