Gọi x 1 , x 2 là hai nghiệm của phương trình x 2 - 5 x + 6 = 0 Tính giá trị của A = 5 x 1 + 5 x 2
A. A = 125
B. A = 3125
C. A = 150
D. A = 15625
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

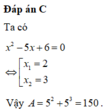

a: \(\text{Δ}=\left(2m-2\right)^2-4\left(2m-5\right)\)
\(=4m^2-8m+4-8m+20\)
\(=4m^2-16m+24\)
\(=4m^2-16m+16+8\)
\(=\left(2m-4\right)^2+8>0\forall m\)
Do đó: Phương trình luôn có hai nghiệm phân biệt
b: Theo đề, ta có: 2(m-1)=6
=>m-1=3
=>m=4

x2 - 2( m + 1 )x + 2m - 4 = 0
1. Δ = b2 - 4ac = [ -2( m + 1 ) ]2 - 4( 2m - 4 )
= 4( m + 1 )2 - 8m + 16
= 4( m2 + 2m + 1 ) - 8m + 16
= 4m2 + 8m + 4 - 8m + 16
= 4m2 + 20
Dễ nhận thấy Δ ≥ 20 > 0 ∀ m
hay phương trình luôn có nghiệm với mọi m ( đpcm )
2. Dù là nghiệm kép hay nghiệm phân biệt thì hai nghiệm của phương trình đều viết được dưới dạng
\(\hept{\begin{cases}x_1=\frac{-b+\sqrt{\text{Δ}}}{2a}=\frac{2m+2+\sqrt{4m^2+20}}{2}\\x_2=\frac{-b-\sqrt{\text{Δ}}}{2a}=\frac{2m+2-\sqrt{4m^2+20}}{2}\end{cases}}\)
Khi đó \(x_1^2+x_2^2=\left(\frac{2m+2+\sqrt{4m^2+20}}{2}\right)^2+\left(\frac{2m+2-\sqrt{4m^2+20}}{2}\right)^2\)
\(=\left(\frac{2m+2+2\sqrt{m^2+5}}{2}\right)^2+\left(\frac{2m+2-2\sqrt{m^2+5}}{2}\right)^2\)( em đưa 2 ra ngoài căn chắc chị hiểu )
\(=\left(\frac{2\left(m+1+\sqrt{m^2+5}\right)}{2}\right)^2+\left(\frac{2\left(m+1-\sqrt{m^2+5}\right)}{2}\right)^2\)
\(=\left(m+1+\sqrt{m^2+5}\right)^2+\left(m+1-\sqrt{m^2+5}\right)^2\)
\(=\left[\left(m+1\right)+\sqrt{m^2+5}\right]^2+\left[\left(m+1\right)-\sqrt{m^2+5}\right]^2\)
\(=\left(m+1\right)^2+2\left(m+1\right)\sqrt{m^2+5}+m^2+5+\left(m+1\right)^2-2\left(m+1\right)\sqrt{m^2+5}+m^2+5\)
\(=2\left(m+1\right)^2+2m^2+10\)
\(=2\left(m^2+2m+1\right)+2m^2+10\)
\(=2m^2+4m+2+2m^2+10=4m^2+4m+12\)
3. Em mới lớp 8 nên chưa học Min Max mấy dạng này chị thông cảm :(((((((((
à xin phép em sửa một tí :))
1. ... = 4m2 + 20
Dễ nhận thấy Δ ≥ 20 > 0 ∀ m
hay phương trình luôn có hai nghiệm phân biệt với mọi m ( đpcm )
2. Vì phương trình luôn có hai nghiệm phân biệt nên hai nghiệm đó luôn viết được dưới dạng : ...
em quên nhìn cái " luôn có hai nghiệm phân biệt " sorry chị :(

Theo điều kiện của bài toán, nghiệm của phương trình (2) bằng một phần ba nghiệm của phương trình (1) nên nghiệm đó bằng 2.
Suy ra, phương trình (3) có nghiệm x = 2
Thay giá trị x = 2 vào phương trình này, ta được (a − 2)2 = a + 3.
Ta coi đây là phương trình mới đối với ẩn a. Giải phương trình mới này: (a − 2)2 = a + 3 ⇔ a = 7
Khi a = 7, dễ thử thấy rằng phương trình (a − 2)x = a + 3 có nghiệm x = 2, nên phương trình (2) cũng có nghiệm x = 2.

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=1\end{matrix}\right.\)
\(A=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=3^2-2.1=7\)

\(x^2-4x-6=0\)
\(\text{Δ}=\left(-4\right)^2-4\cdot1\cdot\left(-6\right)=16+24=40>0\)
=>Phương trình này có hai nghiệm phân biệt
Theo vi-et, ta có:
\(x_1+x_2=\dfrac{-b}{a}=\dfrac{-\left(-4\right)}{1}=4;x_1\cdot x_2=\dfrac{c}{a}=\dfrac{-6}{1}=-6\)
\(A=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=4^2-2\cdot\left(-6\right)=16+12=28\)
\(B=\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{x_1+x_2}{x_1\cdot x_2}=\dfrac{4}{-6}=-\dfrac{2}{3}\)
\(C=x_1^3+x_2^3\)
\(=\left(x_1+x_2\right)^3-3\cdot x_1\cdot x_2\cdot\left(x_1+x_2\right)\)
\(=4^3-3\cdot4\cdot\left(-6\right)=64+72=136\)
\(D=\left|x_1-x_2\right|\)
\(=\sqrt{\left(x_1-x_2\right)^2}\)
\(=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}\)
\(=\sqrt{4^2-4\cdot\left(-6\right)}=\sqrt{16+24}=\sqrt{40}=2\sqrt{10}\)

\(\text{Δ}=\left(2m-2\right)^2-4\left(m-5\right)\)
=4m^2-8m+4-4m+20
=4m^2-12m+24
=4m^2-12m+9+15
=(2m-3)^2+15>0
=>PT luôn có hai nghiệm
A=(x1+x2)^2-2x1x2
=(2m-2)^2-2(m-5)
=4m^2-8m+4-2m+10
=4m^2-10m+14
=4(m^2-5/2m+7/2)
=4(m^2-2*m*5/4+25/16+31/16)
=4(m-5/4)^2+31/4>=31/4
Dấu = xảy ra khi m=5/4