Cho biểu thức B = my 3 − my 2 y + 4 + m 4 y + 1 y − m với m là tham số.
a) Rút gọn B.
b) Khi m = 3 , tìm y để B = 0.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
4 tháng 4 2017
Đúng(0)
Những câu hỏi liên quan
12 tháng 2 2021
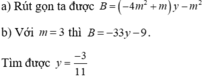
a) Thay m=3 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}x-3y=1\\x+y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4y=-8\\x+y=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=9-y\\y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=7\\y=2\end{matrix}\right.\)
Vậy: Khi m=3 thì hệ phương trình có nghiệm duy nhất là \(\left\{{}\begin{matrix}x=7\\y=2\end{matrix}\right.\)
b) Để hệ phương trình có nghiệm duy nhất thì \(\dfrac{1}{1}\ne\dfrac{-m}{1}\)
\(\Leftrightarrow-m\ne1\)
hay \(m\ne-1\)
Vậy: Để hệ phương trình có nghiệm duy nhất thì \(m\ne-1\)
c) Để hệ phương trình có vô số nghiệm thì \(\dfrac{1}{1}=\dfrac{-m}{1}=\dfrac{1}{m^2}\)
\(\Leftrightarrow\left\{{}\begin{matrix}-m=1\\m^2=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=-1\\m\in\left\{1;-1\right\}\end{matrix}\right.\Leftrightarrow m=-1\)
Vậy: Để hệ phương trình có vô số nghiệm thì m=-1
19 tháng 12 2023
Câu 1:
\(A=\left(2\sqrt{3}+4\cdot\sqrt{27}-\sqrt{108}\right):2\sqrt{3}\)
\(=\dfrac{\left(2\sqrt{3}+4\cdot3\sqrt{3}-6\sqrt{3}\right)}{2\sqrt{3}}\)
\(=\dfrac{2\sqrt{3}+12\sqrt{3}-6\sqrt{3}}{2\sqrt{3}}=\dfrac{8\sqrt{3}}{2\sqrt{3}}=4\)
\(B=\sqrt{9+4\sqrt{5}}-2\left(\sqrt{5}+1\right)\)
\(=\sqrt{5+2\cdot\sqrt{5}\cdot2+4}-2\left(\sqrt{5}+1\right)\)
\(=\sqrt{\left(\sqrt{5}+2\right)^2}-2\left(\sqrt{5}+1\right)\)
\(=\sqrt{5}+2-2\sqrt{5}-2=-\sqrt{5}\)
Câu 2:
a: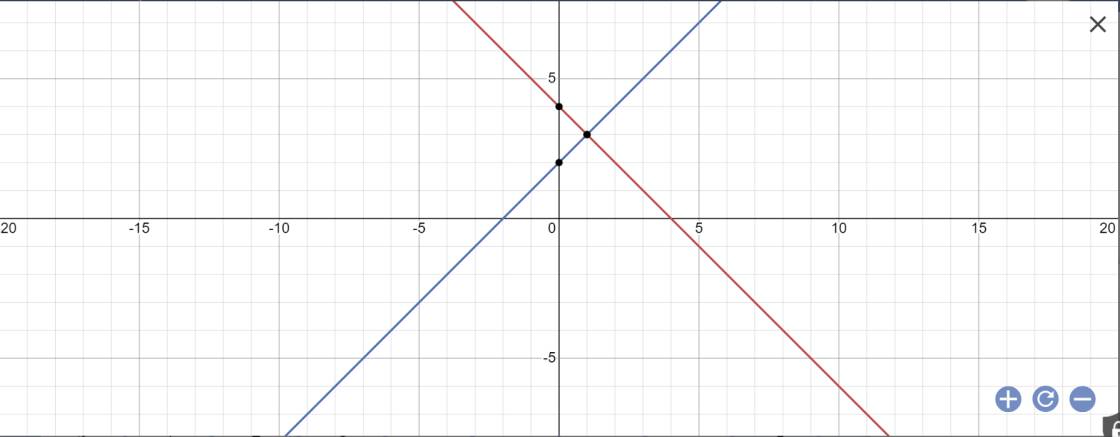 
b: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}x+2=-x+4\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=2\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1+2=3\end{matrix}\right.\)
Thay x=1 và y=3 vào (d3), ta được:
\(m\cdot1+m=3\)
=>2m=3
=>\(m=\dfrac{3}{2}\)
Câu 4:
a: Xét (O) có
ΔCAB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
Xét tứ giác CMON có \(\widehat{CMO}=\widehat{CNO}=\widehat{MCN}=90^0\)
=>CMON là hình chữ nhật
b: Ta có: ΔCAB vuông tại C
=>CA\(\perp\)CB tại C
=>AC\(\perp\)EB tại C
Xét ΔAEB vuông tại A có AC là đường cao
nên \(EC\cdot CB=AC^2\left(1\right)\)
Xét ΔCAB vuông tại C có CH là đường cao
nên \(AH\cdot AB=AC^2\left(2\right)\)
Từ (1) và (2) suy ra \(EC\cdot CB=AH\cdot AB\)
c: Ta có: ΔOAC cân tại O
mà OM là đường cao
nên OM là phân giác của góc AOC
Xét ΔOAI và ΔOCI có
OA=OC
\(\widehat{AOI}=\widehat{COI}\)
OI chung
Do đó: ΔOAI=ΔOCI
=>\(\widehat{OAI}=\widehat{OCI}=90^0\)
Ta có: ΔOBC cân tại O
mà ON là đường cao
nên ON là phân giác của góc COB
Xét ΔOBF và ΔOCF có
OB=OC
\(\widehat{BOF}=\widehat{COF}\)
OF chung
Do đó: ΔOBF=ΔOCF
=>\(\widehat{OBF}=\widehat{OCF}=90^0\)
Ta có: \(\widehat{ICF}=\widehat{ICO}+\widehat{FCO}\)
\(=90^0+90^0=180^0\)
=>I,C,F thẳng hàng
=>OC\(\perp\)IF tại C
Xét (O) có
OC là bán kính
IF\(\perp\)OC tại O
Do đó: IF là tiếp tuyến của (O)
9 tháng 1 2023
a: \(M=\dfrac{-y+4}{y-2}+\dfrac{1}{y-2}+\dfrac{3}{y+2}\)
\(=\dfrac{-y+5}{y-2}+\dfrac{3}{y+2}=\dfrac{-y^2-2y+5y+10+3y-6}{\left(y-2\right)\left(y+2\right)}\)
\(=\dfrac{-y^2+6y+4}{\left(y-2\right)\left(y+2\right)}\)
b: Khi y=3 thì \(M=\dfrac{-3^2+6\cdot3+4}{\left(3-2\right)\left(3+2\right)}=\dfrac{-5+18}{5}=\dfrac{13}{5}\)
3 tháng 1 2021
Bài 1:
a) Ta có: \(P=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{2+5\sqrt{x}}{4-x}\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\cdot\left(\sqrt{x}+2\right)}+\dfrac{2\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}-\dfrac{2+5\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-2-5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{3x-6\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\)
b)
ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne4\end{matrix}\right.\)
Để P=2 thì \(\dfrac{3\sqrt{x}}{\sqrt{x}+2}=2\)
\(\Leftrightarrow3\sqrt{x}=2\left(\sqrt{x}+2\right)\)
\(\Leftrightarrow3\sqrt{x}=2\sqrt{x}+4\)
\(\Leftrightarrow3\sqrt{x}-2\sqrt{x}=4\)
\(\Leftrightarrow\sqrt{x}=4\)
hay x=16(nhận)
Vậy: Để P=2 thì x=16
HP
3 tháng 1 2021
2.
a, \(m=3\), hệ phương trình trở thành:
\(\left\{{}\begin{matrix}x+3y=9\\3x-3y=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x=13\\y=\dfrac{3x-4}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{13}{4}\\y=\dfrac{23}{12}\end{matrix}\right.\)
b, \(\left(x;y\right)=\left(-1;3\right)\) là nghiệm của hệ, suy ra:
\(\left\{{}\begin{matrix}-1+3m=9\\-m-9=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{10}{3}\\m=-13\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại giá trị m thỏa mãn
28 tháng 2 2021
ĐKXĐ: \(m\ne-\dfrac{1}{3}\)
a) Để (P) đi qua điểm \(E\left(\dfrac{1}{2};\dfrac{1}{4}\right)\) thì
Thay \(x=\dfrac{1}{2}\)và \(y=\dfrac{1}{4}\) vào hàm số \(y=\left(3m+1\right)x^2\), ta được:
\(\left(3m+1\right)\cdot\dfrac{1}{4}=\dfrac{1}{4}\)
\(\Leftrightarrow3m+1=1\)
\(\Leftrightarrow3m=0\)
hay m=0(thỏa ĐK)
b) Ta có: \(\left\{{}\begin{matrix}3x-4y=2\\-4x+3y=-5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}12x-16y=8\\-12x+9y=-15\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-7y=-7\\3x-4y=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=1\\3x=2+4y=2+4=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
Vậy: F(2;1)
Để (P) đi qua điểm F(2;1) thì
Thay x=2 và y=1 vào hàm số \(y=\left(3m+1\right)x^2\), ta được:
\(\left(3m+1\right)\cdot4=1\)
\(\Leftrightarrow3m+1=\dfrac{1}{4}\)
\(\Leftrightarrow3m=-\dfrac{3}{4}\)
\(\Leftrightarrow m=\dfrac{-3}{4}:3=\dfrac{-3}{4}\cdot\dfrac{1}{3}=\dfrac{-1}{4}\)(thỏa ĐK)
23 tháng 12 2023
a: Thay m=-2 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}x-2y=-2+1=-1\\-2x+y=3\cdot\left(-2\right)-1=-7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-4y=-2\\-2x+y=-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3y=-9\\x-2y=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=3\\x=2y-1=2\cdot3-1=5\end{matrix}\right.\)
b: Để hệ có nghiệm duy nhất thì \(\dfrac{1}{m}\ne\dfrac{m}{1}\)
=>\(m^2\ne1\)
=>\(m\notin\left\{1;-1\right\}\)
\(\left\{{}\begin{matrix}x+my=m+1\\mx+y=3m-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=m+1-my\\m\left(m+1-my\right)+y=3m-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=m+1-my\\m^2+m-m^2y+y=3m-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=m+1-my\\y\left(-m^2+1\right)=3m-1-m^2-m=-m^2+2m-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=m+1-my\\y\left(m-1\right)\left(m+1\right)=\left(m-1\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{m-1}{m+1}\\x=m+1-m\cdot\dfrac{m-1}{m+1}=\left(m+1\right)-\dfrac{m^2-m}{m+1}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{m-1}{m+1}\\x=\dfrac{m^2+2m+1-m^2+m}{m+1}=\dfrac{3m+1}{m+1}\end{matrix}\right.\)
\(x^2-y^2=4\)
=>\(\dfrac{\left(3m+1\right)^2-\left(m-1\right)^2}{\left(m+1\right)^2}=4\)
=>\(\dfrac{9m^2+6m+1-m^2+2m+1}{\left(m+1\right)^2}=4\)
=>\(8m^2+8m+2=4\left(m+1\right)^2\)
=>\(8m^2+8m+2-4m^2-8m-4=0\)
=>\(4m^2-2=0\)
=>\(m^2=\dfrac{1}{2}\)
=>\(m=\pm\dfrac{1}{\sqrt{2}}\)
2 tháng 10 2018
Bài 1:
a.\(\left(x+y\right)^2-\left(x-y\right)^2=\left(x+y-x+y\right)\left(x+y+x-y\right)=2\left(x+y\right)\)
b.\(2\left(x+y\right)\left(x-y\right)+\left(x+y\right)^2+\left(x-y\right)^2=\left(x+y+x-y\right)^2=4x^2\)